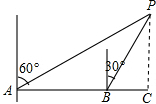
题目内容
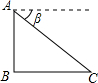
如图，△ABC是等腰三角形，∠ACB=90°，过BC的中点D作DE⊥AB，垂足为E，连接CE，求sin∠ACE的值．
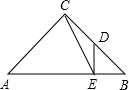
∵△ABC是等腰三角形，∠ACB=90°，
∴∠B=∠A=45°．
∵DE⊥AB，
∴∠EDB=45°．
过点E作EF⊥AC于F，则∠CFE=90°．
设BE=x，则DE=x，BD=
x，
∵D是BC的中点，
∴BC=2
x=AC，
∴AB=4x，AE=3x，
∵EF⊥AC，BC⊥AC，
∴EF∥BC，
∴
=
，即
=
，
解得：EF=
x．
∴CF=
x．
∴CE=
x．
∴sin∠ACE=
=
．
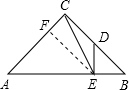
∴∠B=∠A=45°．
∵DE⊥AB，
∴∠EDB=45°．
过点E作EF⊥AC于F，则∠CFE=90°．
设BE=x，则DE=x，BD=
| 2 |
∵D是BC的中点，
∴BC=2
| 2 |
∴AB=4x，AE=3x，
∵EF⊥AC，BC⊥AC，
∴EF∥BC，
∴
| EF |
| BC |
| AE |
| AB |
| EF | ||
2
|
| 3x |
| 4x |
解得：EF=
3
| ||
| 2 |
∴CF=
| ||
| 2 |
∴CE=
| 5 |
∴sin∠ACE=
| EF |
| CE |
3
| ||
| 10 |
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
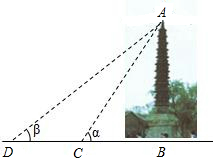
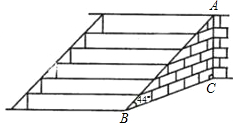把倾角由44°减至32°，已知原台阶AB的长为5米（BC所在地面为水平面）．
