题目内容
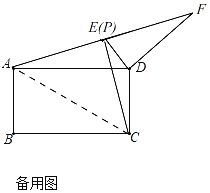
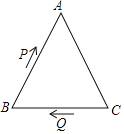
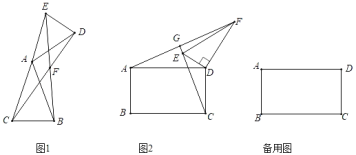
【题目】(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=30°,连接CD,BE交于点F.![]() = ;∠BFD= ;
= ;∠BFD= ;
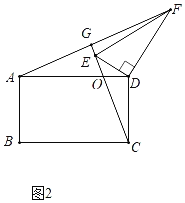
(2)如图2,在矩形ABCD和△DEF中,AB=![]() AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求
AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求![]() 的值及∠AGC的度数,并说明理由.
的值及∠AGC的度数,并说明理由.
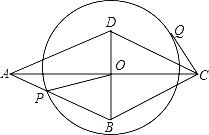
(3)在(2)的条件下,将△DEF绕点D在平面内旋转,AF,CE所在直线交于点P,若DE=1,AD=![]() ,求出当点P与点E重合时AF的长.
,求出当点P与点E重合时AF的长.
【答案】(1)1,150°;(2)![]() ,∠AGC=90°,见解析;(3)6
,∠AGC=90°,见解析;(3)6
【解析】
(1)利用SAS判断出![]() 得出CD=BE,再用数据线的外角和三角形的内角和定理,即可得出结论.
得出CD=BE,再用数据线的外角和三角形的内角和定理,即可得出结论.
(2)先判断出![]() 进而判断出△ADF∽△CDE,即可得出结论.
进而判断出△ADF∽△CDE,即可得出结论.
(3)先求出EF=2,设出CE,进而表示出AE,分两种情况:用勾股定理求出CE,即可得出结论.
解:(1)∵∠BAC=∠DAE=30°,
∴∠BAC+∠BAD=∠DAE+∠BAD,
∴∠CAD=∠BAE,
∵AC=AB,AD=AE,
∴△CAD≌△BAE(SAS),
∴CD=BE,
∴![]() =1,
=1,
∵△CAD≌△BAE(SAS),
∴∠ACD=∠ABE,
∴∠BFD=∠DCB+∠CBE=∠DCB+∠ABE+∠ABC=∠DCB+∠ACD+∠ABC=∠ACB+∠ABC=180°﹣∠BAC=150°,
故答案为1,150°;
(2)如图2,∵四边形ABCD是矩形,
∴∠ADC=90°,AB=CD,
∵AB=![]() AD,
AD,
∴![]() =
=![]() ,
,
在Rt△DEF中,∠DEF=60°,
∴tan∠DEF=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵∠EDF=90°=∠ADC,
∴∠ADF=∠CDE,
∴△ADF∽△CDE,
∴![]() ,∠DAF=∠DCE,
,∠DAF=∠DCE,
AD与CD的交点记作点O,
∵∠DCE+∠COD=90°,
∴∠DAF+∠AOG=90°,
∴∠AGC=90°;
(3)如备用图,
连接AC,在Rt△ADC中,AD=![]() ,
,
∴AB=![]() AD=
AD=![]() ,
,
根据勾股定理得,AC=2![]() ,
,
由(2)知,![]() ,
,
∴AF=![]() CE,
CE,
设CE=x.则AF=![]() x,
x,
在Rt△DEF中,∠DEF=60°,DE=1,
∴EF=2,
∴AE=AF﹣EF=![]() x﹣2,
x﹣2,
由(2)知,∠AEC=90°,
在Rt△ACE中,AE2+CE2=AC2,
∴(![]() x﹣2)2+x2=28,
x﹣2)2+x2=28,
∴x=﹣![]() (舍)或x=2
(舍)或x=2![]() ,
,
∴AF=![]() x=6.
x=6.