题目内容
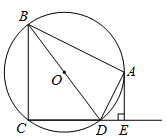
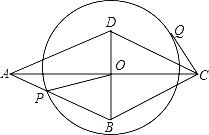
【题目】如图：已知菱形ABCD中，对角线AC和BD相交于点O，AC＝8，BD＝6，动点P在边AB上运动，以点O为圆心，OP为半径作⊙O，CQ切⊙O于点Q．则在点P运动过程中，切线CQ的长的最大值为_____．
【答案】
【解析】
首先连接OQ，由CQ切⊙O于点Q，可得当OQ最小时，CQ最大，即当OP⊥AB时，CQ最大，然后由菱形与直角三角形的性质，求得OP的长，继而求得答案．
解：连接OQ，
∵CQ切⊙O于点Q，
∴OQ⊥CQ，
∴∠CQO＝90°，
∴CQ＝
，
∵四边形ABCD是菱形，
∴AC⊥BD，OA＝OC＝
AC＝×8＝4，OB＝BD＝×6＝3，
∴AB＝
＝5，
∴OC是定值，则当OQ最小时，CQ最大，
即OP最小时，CQ最大，
∴当OP⊥AB时，CQ最大，
此时OQ＝OP＝
∴CQ＝
．
故答案为：．
练习册系列答案
相关题目
