题目内容
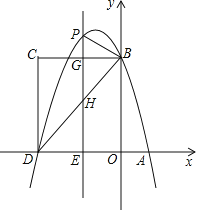
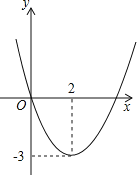
【题目】如图,在坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() .
.
![]() 抛物线的解析式为 .直线
抛物线的解析式为 .直线![]() 的解析式为 ;
的解析式为 ;
![]() 若直线
若直线![]() 与抛物线只有一个公共点,求直线
与抛物线只有一个公共点,求直线![]() 的解析式;
的解析式;
![]() 设抛物线的顶点关于
设抛物线的顶点关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,如果直线
是抛物线对称轴上一动点,如果直线![]() 与抛物线在
与抛物线在![]() 轴上方的部分形成了封闭图形(记为图形
轴上方的部分形成了封闭图形(记为图形![]() ).请结合函数的图象,直接写出点
).请结合函数的图象,直接写出点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将两点坐标直接代入可求出b,c的值,进而求出抛物线解析式为![]() ,得出C的坐标,从而求出直线AC的解析式为y=x+3.
,得出C的坐标,从而求出直线AC的解析式为y=x+3.
(2)设直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与抛物线只有一个公共点,方程
与抛物线只有一个公共点,方程![]() 有两个相等的实数根,再利用根的判别式即可求出b的值.
有两个相等的实数根,再利用根的判别式即可求出b的值.
(3)抛物线的顶点坐标为(-1,4),关于y轴的对称点为M(1,4),可确定M在直线AC上,分直线![]() 不在直线
不在直线![]() 下方和直线
下方和直线![]() 在直线
在直线![]() 下方两种情况分析即可得解.
下方两种情况分析即可得解.
解:![]() 将A,B坐标代入解析式得出b=-2,c=3,
将A,B坐标代入解析式得出b=-2,c=3,
∴抛物线的解析式为:![]()
当x=0 时,y=3,C的坐标为(0,3),
根据A,C坐标可求出直线AC的解析式为y=x+3.
![]()
![]() 直线
直线![]() ,
,
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() .
.
![]() 直线
直线![]() 与抛物线只有一个公共点,
与抛物线只有一个公共点,
![]() 方程
方程![]() 有两个相等的实数根,
有两个相等的实数根,
![]()
![]() ,
,
解得![]() .
.
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
![]()
![]() .
.
解析:如图所示,![]() ,
,
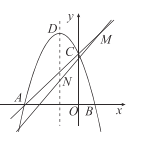
![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() .
.
![]() 抛物线的顶点
抛物线的顶点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上.
上.
①当直线![]() 不在直线
不在直线![]() 下方时,直线
下方时,直线![]() 能与抛物线在第二象限的部分形成封闭图形.
能与抛物线在第二象限的部分形成封闭图形.
当![]() 时,
时,![]() .
.
当直线![]() 与直线
与直线![]() 重合,即动点
重合,即动点![]() 落在直线
落在直线![]() 上时,点
上时,点![]() 的坐标为
的坐标为![]() .
.
随着点![]() 沿抛物线对称轴向上运动,图形
沿抛物线对称轴向上运动,图形![]() 逐渐变小,直至直线
逐渐变小,直至直线![]() 与
与![]() 轴平行时,图形
轴平行时,图形![]() 消失,此时点
消失,此时点![]() 与抛物线的顶点重合,动点
与抛物线的顶点重合,动点![]() 的坐标是
的坐标是![]() ,
,
②当直线![]() 在直线
在直线![]() 下方时,直线
下方时,直线![]() 不能与抛物线的任何部分形成封闭图形.
不能与抛物线的任何部分形成封闭图形.
综上,点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目