题目内容
【题目】阅读下题和解题过程:化简![]() ,使结果不含绝对值.
,使结果不含绝对值.
解:当![]() 时,即
时,即![]() 时,
时,
原式![]()
![]() ;
;
当![]() ,即
,即![]() 时,
时,
原式![]()
![]()
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:![]() ;
;
(2)试探究:当![]() 分别为何值时,方程
分别为何值时,方程![]()
①无解,②只有一个解,③有两个解
【答案】(1)![]() 或
或![]() ;(2)①当
;(2)①当![]() 时方程 无解
时方程 无解![]() 无解;②当
无解;②当![]() 时方程
时方程![]() 只有一个解;③当
只有一个解;③当![]() 时方程
时方程![]() 有两个解.
有两个解.
【解析】
(1)分当x+2≥0时和当x+2<0时,两种情况分类讨论即可;
(2)分当![]() 0,
0,![]() 和
和![]() 三种情况分类讨论即可.
三种情况分类讨论即可.
(1)解:当![]() 时,即
时,即![]() 时:
时:
原方程可化为:![]()
解这个方程得:![]()
当![]() ,即
,即![]() 时:
时:
原方程可化为:![]()
解这个方程得:![]()
![]() 原方程的解为
原方程的解为![]() 或
或![]()
(2)由绝对值的意义可知![]()
①当![]() 时方程
时方程![]() 无解,
无解,
即:当![]() 时方程 无解
时方程 无解![]() 无解
无解
②当![]() 时方程
时方程![]() 只有一个解,
只有一个解,
即:当![]() 时方程
时方程![]() 只有一个解
只有一个解
③当![]() 时方程
时方程![]() 有两个解,
有两个解,
即:当![]() 时方程
时方程![]() 有两个解
有两个解

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的![]() 名选手的复赛成绩如图所示.
名选手的复赛成绩如图所示.
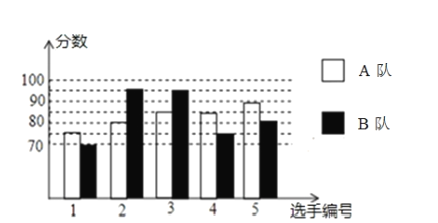
(1)根据图示补全下表;
平均数(分) | 中位数(分) | 众数(分) | |
|
|
| |
|
|
(2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
(3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定.