题目内容
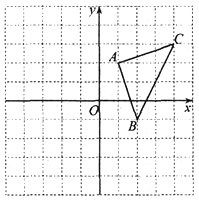
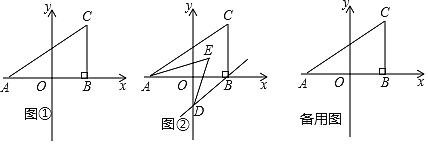
【题目】如图①，在平面直角坐标系中，A
，C
，且满足
过点C作CB⊥
轴于点B.
(1)
(2)在
轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出点P的坐标；若不存在，请说明理由；
(3)如图②，若过点B作BD∥AC交轴于点D，且AE、DE分别平分∠CAB、∠ODB，求∠AED的度数.
【答案】（1）-2；2；4.（2）存在，P点坐标为（0，3），（0，-1）.（3）∠AED =45°.
【解析】
（1）根据非负数的性质得a+2=0，b-2=0，解得a=-2，b=2，则A（-2，0），C（2，2），B（2，0），然后根据三角形面积公式计算S△ABC；
（2）如图③，AC交y轴于Q，先确定Q（0，1），设P（0，t），利用三角形面积公式和S△PAC=S△APQ+S△CPQ=S△ABC得到
|t-1|2+|t-1|2=4，然后解方程求出t即可得到P点坐标；
（3）作EM∥AC，如图②，则AC∥EM∥BD，根据平行线的性质得∠CAE=∠AEM，∠BDE=∠DEM，则∠AED=∠CAE+∠BDE，而∠CAE=∠CAB，∠BDE=∠ODB，所以∠AED=（∠CAB+∠ODB），而由AC∥BD得到∠CAB=∠OBD，于是∠CAB+∠ODB=∠OBD+∠ODB=90°，则∠AED=45°．
解：（1）∵（a+2）2+
=0，
∴a+2=0，b-2=0，解得a=-2，b=2，
∴A（-2，0），C（2，2），
∵CB⊥x轴，
∴B（2，0），
∴S△ABC=×（2+2）×2=4；
故答案为：-2，2，4.
（2）存在．
如图③，AC交y轴于Q，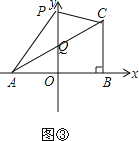 
设Q点坐标为（0，y），依据S△ABC=S△AOQ+S梯形BOQC得：
，
解得y=1，即Q为（0，1）。
设P（0，t），
∵S△PAC=S△APQ+S△CPQ，S△PAC =S△ABC=4，
∴|t-1|2+|t-1|2=4，解得t=3或t=-1，
∴P点坐标为（0，3），（0，-1）；
（3）作EM∥AC，如图②，
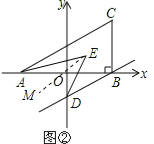
∵AC∥BD，
∴AC∥EM∥BD，
∴∠CAE=∠AEM，∠BDE=∠DEM，
∴∠AED=∠CAE+∠BDE，
∵AE，DE分别平分∠CAB，∠ODB，
∴∠CAE=∠CAB，∠BDE=∠ODB，
∴∠AED=（∠CAB+∠ODB），
∵AC∥BD，
∴∠CAB=∠OBD，
∴∠CAB+∠ODB=∠OBD+∠ODB=90°，
∴∠AED=×90°=45°．
