��Ŀ����
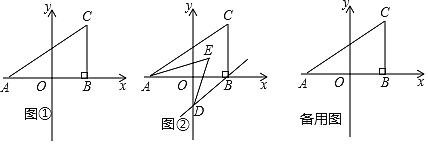
����Ŀ����ͼ�ף��ڵȱ�������ABC����һ��P����PA��2��PB��![]() ��PC��1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
��PC��1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���

������ͬѧ������ͼ�ҵĸ����ߣ�����BPC�Ƶ�B��ʱ����ת60�㣬��ͼ����ʾ������PP�䣬�Ӷ�����õ����������˵���������ɲ������������
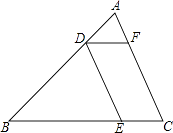
����ͼ������������ABCD����һ��P����PA��![]() ��BP��
��BP��![]() ��PC��1�����BPC�����Ĵ�С��������ABCD�ı߳���
��PC��1�����BPC�����Ĵ�С��������ABCD�ı߳���
���𰸡��ټ�����������BPC�Ķ�����135�㣬������ABCD�ı߳���![]() ��
��
��������
��������ת�ó�AP�䣽CP��1��BP�䣽BP��![]() ����AP��B����BPC�������ABP��+��ABP��60�㣬�õ��ȱߡ�BPP�䣬�Ƴ�PP�䣽PB��
����AP��B����BPC�������ABP��+��ABP��60�㣬�õ��ȱߡ�BPP�䣬�Ƴ�PP�䣽PB��![]() ����BP��P��60�㣬�����AP��P��90�㣬���������BPC������B��BM��AP�䣬��AP����ӳ����ڵ�M���ɡ�MP��B��30�㣬���BM��
����BP��P��60�㣬�����AP��P��90�㣬���������BPC������B��BM��AP�䣬��AP����ӳ����ڵ�M���ɡ�MP��B��30�㣬���BM��![]() ��P��M��
��P��M��![]() �����ݹ��ɶ�����������𰸣�
�����ݹ��ɶ�����������𰸣�
��ͬ�������BEP��![]() ��180�㩁90�㣩��45�㣬���ݹ��ɶ������涨�������AEP��90�㣬�Ƴ���BPC����AEB��90��+45�㣽135�㣻����B��BF��AE����AE���ӳ����ڵ�F�����FE��BF��1��AF��2�����ݹ��ɶ����������AB��
��180�㩁90�㣩��45�㣬���ݹ��ɶ������涨�������AEP��90�㣬�Ƴ���BPC����AEB��90��+45�㣽135�㣻����B��BF��AE����AE���ӳ����ڵ�F�����FE��BF��1��AF��2�����ݹ��ɶ����������AB��
�١ߡ�ABC�ǵȱ������Σ�
���ABC��60�㣬
����BPC�Ƶ�B��ʱ����ת60�㣬��ͼ����ʾ������PP�䣬
��AP�䣽CP��1��BP�䣽BP��![]() ����AP��B����BPC��
����AP��B����BPC��
����ת�ã���P'BP����ABC��60�㣬
���BPP���ǵȱ������Σ�
��PP�䣽PB��![]() ����BP��P��60�㣬
����BP��P��60�㣬
��AP�䣽1��AP��2��
��AP��2+PP��2��AP2��
���AP��P��90�㣬
���BPC����AP��B��90��+60�㣽150�㣬
����B��BM��AP�䣬��AP����ӳ����ڵ�M��
���MP��B��30�㣬BM��![]() P'B��
P'B��![]() ��
��
�ɹ��ɶ����ã�P��M��![]() ��
��![]() ��
��
��AM��AP'+P'M��1+![]() ��
��![]() ��
��
�ɹ��ɶ����ã�AB��![]() ��
��![]() ��
��![]() ��
��
�ڽ���BPC�Ƶ�B��ʱ����ת90��õ���AEB����ͼ����
��(1)���ƣ��ɵã�AE��PC��1��BE��BP��![]() ����BPC����AEB��
����BPC����AEB��
���EBP����ABC��90�㣬
���BEP��45�㣬
�ɹ��ɶ����ã�EP��2��
��AE��1��AP��![]() ��EP��2��
��EP��2��
��AE2+PE2��AP2��
���AEP��90�㣬
���BPC����AEB��90��+45�㣽135�㣬
����B��BF��AE����AE���ӳ����ڵ�F��
���FEB��45�㣬
��FE��BF��1��
��AF��2��
����Rt��ABF�У��ɹ��ɶ�������AB��![]() ��
��![]() ��
��
�𣺡�BPC�Ķ�����135�㣬������ABCD�ı߳���![]() ��
��

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�����Ŀ����������У�ij����ʳ��Ϊ�˱�֤�����ʳ�İ�ȫ���������ס��������ֿ����ʳ��ȫ��ת�Ƶ����н�ǿ�����ܵ�A��B���ֿ⣮��֪������ʳ100�֣��ҿ�����ʳ80�֣���A�������Ϊ70�֣�B�������Ϊ110�֣��Ӽס������A��B�����·�̺��˷����±��������С�Ԫ/��ǧ�ס���ʾÿ����ʳ����1ǧ����������ң�
·�̣�ǧ�ף� | �˷ѣ�Ԫ/��ǧ�ף� | |||
�� | �ҿ� | �� | �ҿ� | |
A�� | 20 | 15 | 12 | 12 |
B�� | 25 | 20 | 10 | 8 |
��1����������A����ʳx�֣���д������ʳ����A��B��������˷�y��Ԫ����x���֣��ĺ�����ϵʽ��
��2�����ס������������A��B������ٶ���ʳʱ�����˷���ʡ����ʡ�����˷��Ƕ��٣�