题目内容
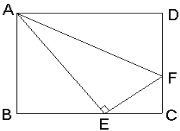
【题目】如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,求CF的长。
【答案】![]() .
.
【解析】
试题分析:证△AEF≌△ADF,推出AE=AD=5,EF=DF,在△ABE中,由勾股定理求出BE=3,求出CE=2,设CF=x,则EF=DF=4-x,在Rt△CFE中,由勾股定理得出方程(4-x)2=x2+22,求出x即可.
试题解析:∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,AD=BC=5,AB=CD=4,
∵EF⊥AE,
∴∠AEF=∠D=90°,
在△AEF和△ADF中,
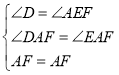 ,
,
∴△AEF≌△ADF(AAS),
∴AE=AD=5,EF=DF,
在△ABE中,∠B=90°,AE=5,AB=4,由勾股定理得:BE=3,
∴CE=5-3=2,
设CF=x,则EF=DF=4-x,
在Rt△CFE中,由勾股定理得:EF2=CE2+CF2,
∴(4-x)2=x2+22,
x=![]() ,
,
CF=![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】某食品店卖大米,数量x(千克)和售价y(元)之间的关系如下:
数量x/千克 | 0.5 | 1 | 1.5 | 2 | … |
售价y/元 | 1.2+0.2 | 2.4+0.2 | 3.6+0.2 | 4.8+0.2 | … |
(1)观察表格,根据规律写出数量量x(千克)与售价y(元)之间的函数关系式;
(2)计算出张阿姨买了6千克的大米,需要付多少钱?