题目内容
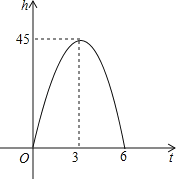
【题目】对于上抛物体，在不计空气阻力的情况下，有如下关系式：h=v0t﹣
gt2，其中h（米）是上抛物体上升的高度，v0（米/秒）是上抛物体的初速度，g（米/秒2）是重力加速度，t（秒）是物体抛出后所经过的时间，如图是h与t的函数关系图．
（1）求：v0和g；
（2）几秒后，物体在离抛出点40米高的地方？
【答案】（1）v0=30（米/秒），g=10（米/秒2）；（2）经过2秒或4秒的物体在离抛出点40米高的地方．
【解析】
试题分析：（1）已知h=v0t﹣
gt2经过的坐标，把坐标代入解析式可解出v0和g；
（2）令h=40，代入方程可解．
解：（1）由图可知，h=v0t﹣gt2的图象经过（6，0）、（3，45）点，
∴
，
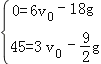解这个方程组，得：
．
∴v0=30（米/秒），g=10（米/秒2）；
（2）由（1）得，函数关系式是h=30t﹣5t2，
当h=40时，则30t﹣5t2=40，
解这个方程，得t1=2，t2=4，
故经过2秒或4秒的物体在离抛出点40米高的地方．
练习册系列答案
相关题目
