题目内容
【题目】综合与实践
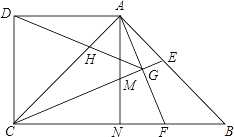
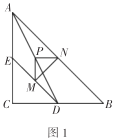
问题情境:在综合与实践课上,老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动,如图1,三角板![]() 和三角板
和三角板![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,连接
上,连接![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.试判断线段
的中点.试判断线段![]() 与
与![]() 的数量关系和位置关系.
的数量关系和位置关系.
探究展示:勤奋小组发现,![]() ,
,![]() .并展示了如下的证明方法:
.并展示了如下的证明方法:
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .(依据1)
.(依据1)
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .(依据2)
.(依据2)
∴![]() .∴
.∴![]() .
.
反思交流:
(1)①上述证明过程中的“依据1”,“依据2”分别是指什么?
②试判断图1中,![]() 与
与![]() 的位置关系,请直接回答,不必证明;
的位置关系,请直接回答,不必证明;
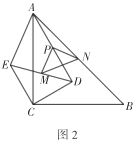
(2)创新小组受到勤奋小组的启发,继续进行探究,把![]() 绕点
绕点![]() 逆时针方向旋转到如图2的位置,发现
逆时针方向旋转到如图2的位置,发现![]() 是等腰直角三角形,请你给出证明;
是等腰直角三角形,请你给出证明;
(3)缜密小组的同学继续探究,把![]() 绕点
绕点![]() 在平面内自由旋转,当
在平面内自由旋转,当![]() ,
,![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
【答案】(1)①依据1:三角形的中位线平行于第三边并且等于第三边的一半.
依据2:直角三角形的两个锐角互余.②![]() . (2)见解析 (3)
. (2)见解析 (3)![]()
【解析】
(1)①根据三角形的中位线的性质和直角三角形的性质,即可得到答案;
②由![]() ,得∠ANP=45°,结合∠PNM=45°,即可得到结论;
,得∠ANP=45°,结合∠PNM=45°,即可得到结论;
(2)连接![]() ,先证
,先证![]() ,得
,得![]() ,
,![]() ,从而得
,从而得![]() 是等腰三角形.通过三角形外角的性质和直角三角形的性质可得
是等腰三角形.通过三角形外角的性质和直角三角形的性质可得![]()
![]() ,进而得
,进而得![]() ,即可得到结论;
,即可得到结论;
(3)由![]() 是等腰直角三角形,
是等腰直角三角形,![]() 可得,当BD最大时,
可得,当BD最大时,![]() 面积最大,进而即可得到答案.
面积最大,进而即可得到答案.
(1)①依据1:三角形的中位线平行于第三边并且等于第三边的一半.
依据2:直角三角形的两个锐角互余.
②![]() .理由如下:
.理由如下:
由勤奋小组发现,![]() ,
,![]() ,可知:PMN是等腰直角三角形,
,可知:PMN是等腰直角三角形,
∴∠PNM=45°,
∵![]() ,
,
∴∠ANP=∠B=45°,
∴∠ANM=45°+45°=90°,即:![]() ;
;
(2)连接![]() ,由旋转的性质知,
,由旋转的性质知,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中位线,
的中位线,
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
又∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(3)由(2)知,![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
∴BD最大时,![]() 面积最大,此时,点
面积最大,此时,点![]() 在
在![]() 的延长线上,即:
的延长线上,即:![]() ,
,
∴PM的最大值为7,
∴![]() 的最大值
的最大值![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案