题目内容
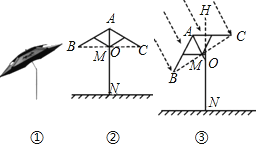
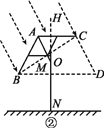
【题目】如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB,AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m,BC与AN交于点M,撑杆AN=2.2m,固定点O到地面的距离ON=1.6m.
(1)如图②,当伞完全撑开并直立时,求点B到地面的距离.
(2)某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明:![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
【答案】(1)点B到地面的距离约为1.6 m;(2)①此时点B到地面的距离约为1.1 m;②BC在水平地面上投影的长度约为2.3 m.
【解析】
(1)求出AM的长即可得出答案;
(2)①过点A,B分别作地面的垂线,垂足分别为Q,T,求出∠ABS=30°,则BS=BM=1.可得BT=OP+ON﹣SB,求出答案;②可知BC⊥CD,∠CBD=30°.可求出BD的长.
解:(1)点B到地面的距离即为MN的长度,
MN=AN﹣AM=AN﹣BMtan30°=2.2﹣![]() ≈1.6(m).
≈1.6(m).
答:点B到地面的距离约为1.6 m.
(2)①如图①,过点A,B分别作地面的垂线,垂足分别为Q,T,
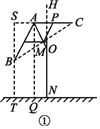
∵∠AOH=30°,
∴∠OAQ=30°.
∵∠ABC=30°,
∴∠BAO=90°﹣∠ABC=60°,
∴∠BAQ=∠BAO﹣∠OAQ=30°,
∴∠ABS=30°,
∴BS=BM=1.
∴BT=OP+ON﹣SB=OAcos30°+ON﹣SB=0.6×![]() +1.6﹣1≈1.1(m).
+1.6﹣1≈1.1(m).
答:此时点B到地面的距离约为1.1 m.
②如图②,依题意,可知BC⊥CD,∠CBD=30°.
∵BC=2,
∴BD=![]() ≈2.3(m).
≈2.3(m).
答:BC在水平地面上投影的长度约为2.3 m.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案