题目内容
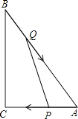
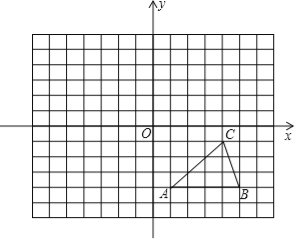
【题目】如图,在![]() 中,弦AB,CD相交于点E,
中,弦AB,CD相交于点E,![]() =
=![]() ,点D在
,点D在![]() 上,连结CO,并延长CO交线段AB于点F,连接OA,OB,且OA=2,∠OBA=30°
上,连结CO,并延长CO交线段AB于点F,连接OA,OB,且OA=2,∠OBA=30°
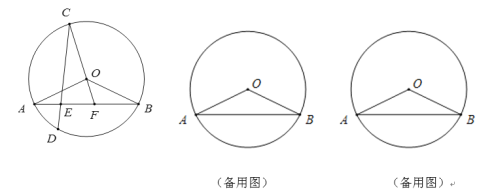
(1)求证:∠OBA=∠OCD;
(2)当![]() AOF是直角三角形时,求EF的长;
AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得![]() ,若存在,请求出EF的长,若不存在,请说明理由.
,若存在,请求出EF的长,若不存在,请说明理由.
【答案】(1)详见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据在“同圆或等圆中,同弧或等弧所对的圆周角相等”可得;(2)分两种情况讨论,当![]() 时,解直角三角形AFO可求得AF和OF的长,再解直角三角形EFC可得;当
时,解直角三角形AFO可求得AF和OF的长,再解直角三角形EFC可得;当![]() 时,解直角三角形AFO可求得AF和OF的长,根据三角函数求解;(3)由边边边定理可证
时,解直角三角形AFO可求得AF和OF的长,根据三角函数求解;(3)由边边边定理可证![]() ,再证
,再证![]() ,根据对应边成比例求解.
,根据对应边成比例求解.
解:(1)延长AO,CO分别交圆于点M,N
![]() 为直径
为直径
![]()
![]() 弧AC=弧BD
弧AC=弧BD
![]() 弧CD=弧AB
弧CD=弧AB
![]()
![]()
![]()

(2)①当![]() 时
时
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
②当![]() 时
时
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
综上所述: ![]() 或
或![]()
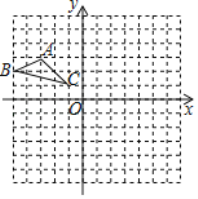
(3)连结![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]()
![]() 弧AC=弧BD
弧AC=弧BD
![]() 弧CD=弧AB
弧CD=弧AB
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()

∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]()
∵![]()
![]()
∴![]()
∴![]()
![]()
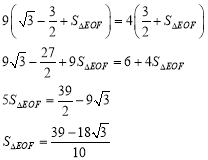
∴![]()
![]()

练习册系列答案
相关题目
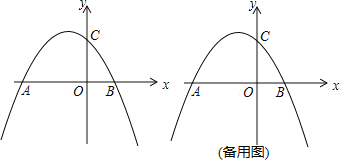
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4;⑤若
有一个根大于4;⑤若![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )
A.①②③B.①②③④⑤C.①③⑤D.①③④⑤