题目内容
【题目】已知抛物线![]() 的对称轴与
的对称轴与![]() 轴的交点横坐标是分式方程
轴的交点横坐标是分式方程![]() 的解,若抛物线与
的解,若抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]()
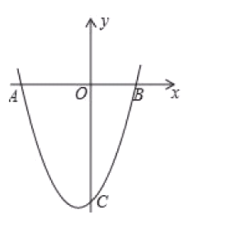
(1)求抛物线![]() 的解析式;
的解析式;
(2)若点![]() 坐标为
坐标为![]() ,连结
,连结![]() ,若点
,若点![]() 是线段
是线段![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.
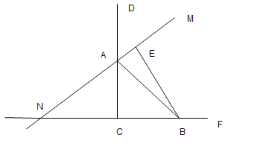
(3)连结![]() 过点
过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 在第三象限中的抛物线上取点
在第三象限中的抛物线上取点![]() 过点
过点![]() 作直线
作直线![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,已知
,已知![]() .
.
①求点![]() 的坐标;
的坐标;
②在抛物线上是否存在一点![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①点
;(3)①点![]() 坐标为
坐标为![]() 点
点![]() 坐标为
坐标为![]() ;②点
;②点![]() 的坐标为
的坐标为![]()
【解析】
(1)通过解方程求出抛物线对称轴的横坐标,得出![]() ,再代入点坐标即可;
,再代入点坐标即可;
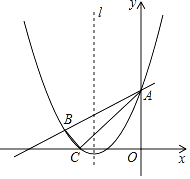
(2)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 过点
过点![]() 作
作![]() 轴交
轴交![]() 与点
与点![]() 、交
、交![]() 轴与点
轴与点![]() ,在图示的位置时,
,在图示的位置时,![]() 有最小值,即可求解;
有最小值,即可求解;
(3)①![]() ,则
,则![]() ,即:
,即:![]() ,求解即可;②求出HP所在的直线表达式与二次函数联立,求得交点即可.
,求解即可;②求出HP所在的直线表达式与二次函数联立,求得交点即可.
解:(1)抛物线对称轴与![]() 轴交点横坐标是
轴交点横坐标是![]() 的解,
的解,
![]() 抛物线对称轴为
抛物线对称轴为![]() ,
,
![]()
![]() 抛物线
抛物线![]() 过点
过点![]()
![]()
![]()
![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]()
(2)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 过点
过点![]() 作
作![]() 轴交
轴交![]() 与点
与点![]() 、交
、交![]() 轴与点
轴与点![]()
![]() ,
,
则![]() ,
,
![]() ,
,
在图示的位置时,![]() ,
,
此时为最小值,长度为![]() ,
,
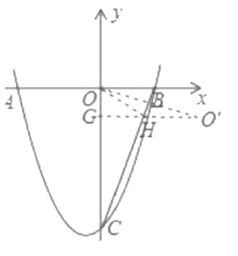
![]() ,,
,,
![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
即![]() 的最小值为
的最小值为![]() ;
;
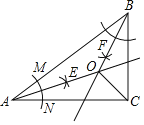
(3)![]() 设点
设点![]() 的坐标为
的坐标为![]() ,
,
直线![]() 表达式
表达式![]() 的值为
的值为![]() ,
,
则直线![]() 表达式
表达式![]() 的值为
的值为![]() ,
,
设直线![]() 的表达式为:
的表达式为:![]()
将点![]() 坐标代入上式并解得:
坐标代入上式并解得:![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
点![]() 的坐标为
的坐标为![]()
过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() 过点
过点![]() 作
作![]() 轴平行线交过
轴平行线交过![]() 点作
点作![]() 轴的平行线于点
轴的平行线于点![]()
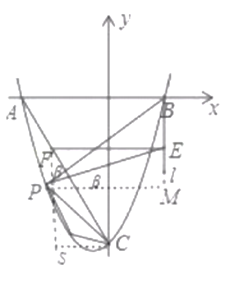
![]() ,
,
![]()
![]() ,
,
则![]() ,
,
即:![]()
![]() ,
,
即:![]() ,
,
解得:![]() 或
或![]() (舍去
(舍去![]() )
)
故点![]() 坐标为
坐标为![]()
点![]() 坐标为
坐标为![]() ;
;
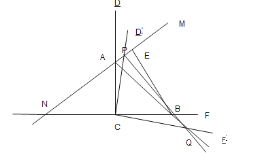
![]() 过点
过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() 、交
、交![]() 轴于点
轴于点![]() ,作
,作![]() 于点
于点![]() ,
,
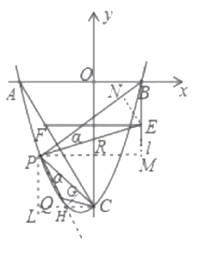
则: ![]()
则![]() ,
,![]() ,
,
设:![]()
则![]()
则![]() ,
,
过点![]() 作
作![]() 轴的平行线交过
轴的平行线交过![]() 点与
点与![]() 轴的平行线于点
轴的平行线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]()
则:![]() ,
,
即四边形![]() 为正方形,
为正方形,
![]() ,
,
设:![]() ,
,
![]() ,
,![]() ,
,
则![]()
![]() 即点
即点![]() 坐标为
坐标为![]() ,
,
则![]() 所在的直线表达式为:
所在的直线表达式为:![]() ,
,
![]() 联立并解得:
联立并解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目