题目内容
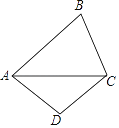
【题目】如图,AB是⊙O的直径,C,D在⊙O上两点,连接AD,CD.
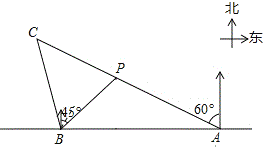
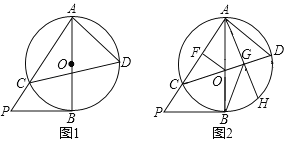
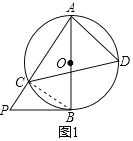
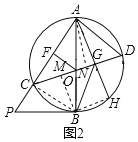
(1)如图1,点P是AC延长线上一点,∠APB=∠ADC,求证:BP与⊙O相切;
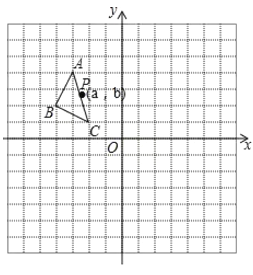
(2)如图2,点G在CD上,OF⊥AC于点F,连接AG并延长交⊙O于点H,若CD为⊙O的直径,当∠CGB=∠HGB,BG=2OF=6时,求⊙O半径的长.
【答案】(1)见解析;(2)2![]()
【解析】
(1)如图1,连接BC,根据圆周角定理得到∠ACB=90°,得到∠ABC=∠P,求得∠ABP=90°,于是得到结论;
(2)如图2中,连接BC,BH,作BM⊥CD于M,AN⊥CD于N.想办法证明OM=ON=GN,MG=DN,设OM=ON=a,构建方程求出a即可解决问题.
解:(1)如图1,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
∵∠ABC=∠D,∠D=∠P,
∴∠ABC=∠P,
∴∠P+∠PAB=90°,
∴∠ABP=90°,
∴BP与⊙O相切;
(2)如图2,连接BC,BH,作BM⊥CD于M,AN⊥CD于N.
∵CD,AB是直径,
∴OA=OD=OC=OB,∵∠AOD=∠BOC,
∴△AOD≌△BOC(SAS),
∴AD=BC=2OF=6,
∵OA=OB,∠AON=∠BOM,∠ANO=∠BMO=90°,
∴△AON≌△BOM(AAS),
∴OM=ON,AN=BM,设OM=ON=a,
∵∠CGB=∠HGB,
∴∠OGH=2∠CGB,
∵∠BOG=∠OCB+∠OBC=2∠GCB,∠GCB=∠BGC,
∴∠BOG=∠OGH,
∴∠AOG=∠AGO,
∴AO=AG,
∵AN⊥OG,
∴ON=NG=a,
∵BG=AD,BM=AN,∠AND=∠BMG=90°,
∴Rt△BMG≌Rt△AND(HL),
∴MG=DN=3a,OD=OA=OB=OC=4a,
∴BM=![]() =
=![]() a,
a,
在Rt△CBM中,∵BC2=BM2+CM2,
∴36=15a2+9a2,
∵a>0,
∴a=![]() ,
,
∴MG=CM=3a=![]() ,
,
∴DG=2a=![]() ,
,
∴CD=2×![]() +
+![]() =4
=4![]() ,
,
∴⊙O半径的长为2![]() .
.

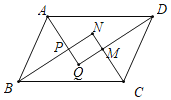
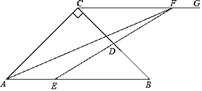
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED,并延长ED交CG于点F,连接AF.设A,E两点间的距离为xcm,A,F两点间的距离为y1cm,E,F两点间的距离为y2cm.小丽根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小丽的探究过程,请补充完整:
(1)按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 9.49 | 8.54 | 7.62 | 6.71 | 5.83 | 5.00 | 4.24 |
y2/cm | 9.49 | 7.62 | 5.83 | 3.16 | 3.16 | 4.24 |
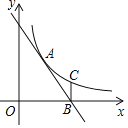
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;

(3)结合函数图象,解决问题:当△AEF为等腰三角形时,AE的长度约为 cm.