Question

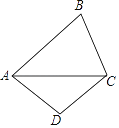
【题目】如图，已知四边形ABCD中，AC平分∠BAD，AB=AC=5，AD=3，BC=CD.则点C到AB的距离是( )

A.B.C.3D.2

Answer 1

【答案】C

【解析】

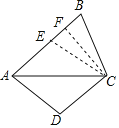
在AB上截取AE=AD=3，连接CE，过C作CF⊥AB于F点，根据SAS定理得出△ADC≌△AEC，故可得出CE=CD，再由垂直平分线的性质求出AF的长，根据勾股定理即可得出结论．

在AB上截取AE=AD=3，连接CE，过C作CF⊥AB于F点．

∵AC平分∠BAD，
∴∠BAC=∠DAC．
在△ADC与△AEC中，

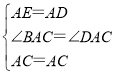
∴△ADC≌△AEC（SAS），
∴CE=CD．
∵CD=CB，
∴CE=CB．
∵CF⊥BE，
∴CF垂直平分BE．
∵AB=5，AE=AD=3
∴BE=2，
∴EF=1，
∴AF=4，
在Rt△ACF中，
∵CF2=AC2-AF2=52-42=9，
∴CF=3．

故选：C