题目内容
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.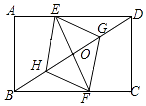
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
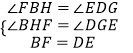 ,
,
∴BFH≌△DEG(AAS)
(2)解:四边形EGFH是菱形;理由如下:
连接DF,如图所示: 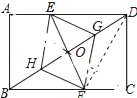
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵DE=BF,∠EOD=∠BOF,∠EDO=∠FBO,
∴△EDO≌△FBO,
∴OB=OD,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
【解析】(1)首先依据平行四边形的性质可得到AD∥BC,AD=BC,OB=OD,接下来,依据平行线的性质证明∠FBH=∠EDG,∠OHF=∠OGE,依据等角的补角相等可得到∠BHF=∠DGE,求出BF=DE,最后由AAS进行证明即可;
(2)首先证明四边形EGFH是平行四边形,接下来,在依据等腰三角形的性质得出EF⊥GH,最后,依据对角线相互垂直的平行四边形是菱形进行证明即可.
【考点精析】本题主要考查了菱形的判定方法和矩形的性质的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
【题目】已知某山区的平均气温与该山的海拔高度的关系见下表:
海拔高度(单位:米) | 0 | 100 | 200 | 300 | 400 | … |
平均气温(单位:℃) | 22 | 21.5 | 21 | 20.5 | 20 | … |
(1)若海拔高度用x(米)表示,平均气温用y(℃)表示,试写出y与x之间的函数关系式;
(2)若某种植物适宜生长在18℃~20℃(包含18℃,也包含20℃)山区,请问该植物适宜种植在海拔为多少米的山区?
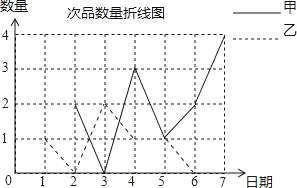
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?