Question

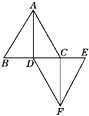
【题目】如图，已知在四边形ABCD中，AD＝BC且AC⊥BD，点E，F，G，H，P，Q分别是AB，BC，CD，DA，AC，BD的中点．

求证：(1)四边形EFGH是矩形；

(2)四边形EQGP是菱形．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）已知点E，F，G，H分别为AB，BC，CD，DA的中点，根据三角形的中位线定理可得EF∥AC，GF∥BD，GH∥AC，EH∥BD，所以EF∥GH，GF∥EH，根据两组对边分别平行的四边形是平行四边形，即可判定四边形EFGH是平行四边形；（2）已知点E，P，G，Q分别为AB，AC，DC，DB的中点，根据三角形的中位线定理可得EP＝BC，PG＝AD，GQ＝BC，QE＝AD，又因AD＝BC，所以EP＝PG＝GQ＝QE，即可判定四边形EQGP是菱形．

试题解析：

(1)∵点E，F，G，H分别为AB，BC，CD，DA的中点，

∴EF∥AC，GF∥BD，GH∥AC，EH∥BD，

∴EF∥GH，GF∥EH，∴四边形EFGH是平行四边形．

又∵AC⊥BD，∴EF⊥EH.∴EFGH是矩形．

(2)∵点E，P，G，Q分别为AB，AC，DC，DB的中点，

∴EP＝BC，PG＝AD，GQ＝BC，QE＝AD.

∵AD＝BC，∴EP＝PG＝GQ＝QE，∴四边形EQGP是菱形．