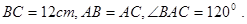题目内容
(本题满分10分)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.

小题1:(1)求证:点D是AB的中点;
小题2:(2)判断DE与⊙O的位置关系,并证明你的结论;
小题3:(3)若⊙O的半径为9,AB=12,求DE的长.

小题1:(1)求证:点D是AB的中点;
小题2:(2)判断DE与⊙O的位置关系,并证明你的结论;
小题3:(3)若⊙O的半径为9,AB=12,求DE的长.
小题1:(1)证明:连接CD

∵BC为直径的⊙O
 ∴ CD⊥AB
∴ CD⊥AB∵BC=AC ∴AD=BD
即点D是AB的中点
小题2:(2)DE与⊙O相切
∵AD=BD OB="OC " ∴OD∥AC
∵DE⊥AC ∴ OD⊥DE
∴DE与⊙O相切
小题3:(3)∵CD⊥AB DE⊥AC
 ∴△AED∽△ADC
∴△AED∽△ADC∴
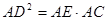
∵
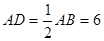 ,
,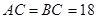 ∴
∴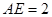
∴
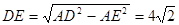
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
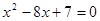 的两个根,且O1O2=7,则⊙O1、⊙O2的位置关系是
的两个根,且O1O2=7,则⊙O1、⊙O2的位置关系是
 中,
中,