题目内容
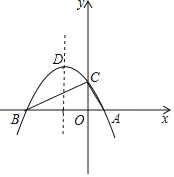
【题目】如图,已知∠AOC=∠BOD=120°,∠BOC=![]() ∠AOD.
∠AOD.
(1)求∠AOD的度数;
(2)若射线OB绕点O以每秒旋转20°的速度顺时针旋转,同时射线OC以每秒旋转15°的速度逆时针旋转,设旋转的时间为t秒(0<t<6),试求当∠BOC=20°时t的值;
(3)若∠AOB绕点O以每秒旋转5°的速度逆时针旋转,同时∠COD绕点O以每秒旋转10°的速度逆时针旋转,设旋转的时间为t秒(0<t<18),OM平分∠AOC,ON平分∠BOD,在旋转的过程中,∠MON的度数是否发生改变?若不变,求出其值:若改变,说明理由.

【答案】(1)∠AOD=150°;(2)t=2或t=![]() ;(3)∠MON的度数不会发生改变,∠MON=30°,理由见解析.
;(3)∠MON的度数不会发生改变,∠MON=30°,理由见解析.
【解析】
(1)由角的和差倍分构建方程求出∠AOD的度数为150°;
(2)分两射线重合前后两种情况,建立等量关系求出时间分别为t=2或t=![]() ;
;
(3)由角度的旋转求出旋转角的大小,角的和差,角平分线的定义求出∠MON的度数为30°.
解:如图所示:
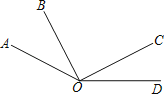
(1)设∠AOD=5x°,
∵∠BOC=![]() ∠AOD
∠AOD
∴∠BOC=![]() 5x°=3x°
5x°=3x°
又∵∠AOC=∠AOB+∠BOC,∠BOD=∠DOC+∠BOC,
∠AOD=∠AOB+∠BOC+∠DOC,
∴∠AOC+∠BOD=∠AOD+∠BOC,
又∵∠AOC=∠BOD=120°,
∴5x+3x=240
解得:x=30°
∴∠AOD=150°;
(2)∵∠AOD=150°,∠BOC=![]() ∠AOD,
∠AOD,
∴∠BOC=90°,
①若线段OB、OC重合前相差20°,则有:
20t+15t+20=90,
解得:t=2,
②若线段OB、OC重合后相差20°,则有:
20t+15t﹣90=20
解得:t=![]() ,
,
又∵0<t<6,
∴t=2或t=![]() ;
;
(3)∠MON的度数不会发生改变,∠MON=30°,理由如下:
∵旋转t秒后,∠AOD=150°﹣5t°,∠AOC=120°﹣5t°,∠BOD=120°﹣5t°
∵OM、ON分别平分∠AOC、∠BOD
∴∠AOM=![]() ∠AOC=
∠AOC=![]() ,
,
∠DON=![]() ∠BOD=
∠BOD=![]()
∴∠MON=∠AOD﹣∠AOM﹣∠DON
=150°﹣5t°﹣![]() ﹣
﹣![]()
=30°.