题目内容
【题目】如图,在![]() 中,
中,![]() ,E为CA延长线上一点,D为AB上一点,F为
,E为CA延长线上一点,D为AB上一点,F为![]() 外一点且
外一点且![]() 连接DF,BF.
连接DF,BF.
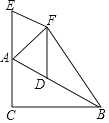
(1)当![]() 的度数是多少时,四边形ADFE为菱形,请说明理由:
的度数是多少时,四边形ADFE为菱形,请说明理由:
(2)当AB= 时,四边形ACBF为正方形(请直接写出)
【答案】(1)当![]() 时,四边形ADFE为菱形,理由详见解析; (2)
时,四边形ADFE为菱形,理由详见解析; (2)![]() .
.
【解析】
(1)当∠CAB=60°时,四边形ADFE为菱形;由平行线的性质可证∠AFE=∠DAF,∠AEF=∠CAB=60°,可得△AEF,△AFD都是等边三角形,可得AE=AF=AD=EF=FD,即可得结论.
(2)由正方形的性质可求解.
(1)当∠CAB=60°时,四边形ADFE为菱形,
理由如下:
∵AE=AF=AD
∴∠AEF=∠AFE,
∵EF∥AB
∴∠AFE=∠DAF,∠AEF=∠CAB=60°
∴∠FAD=60°
∴△AEF,△AFD都是等边三角形
∴AE=AF=AD=EF=FD
∴四边形ADFE为菱形
(2)若四边形ACBF为正方形
∴AC=BC=1,∠ACB=90°
∴AB=![]()
∴当AB=![]() 时,四边形ACBF为正方形
时,四边形ACBF为正方形
故答案为:![]()

练习册系列答案
相关题目