题目内容
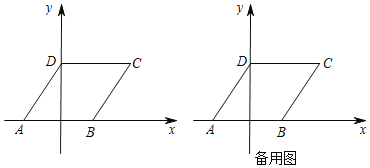
【题目】如图,ABCD在平面直角坐标系中,点A(﹣2,0),点B(2,0),点D(0,3),点C在第一象限.
(1)求直线AD的解析式;
(2)若E为y轴上的点,求△EBC周长的最小值;
(3)若点Q在平面直角坐标系内,点P在直线AD上,是否存在以DP,DB为邻边的菱形DBQP?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)△EBC周长的最小值为
;(2)△EBC周长的最小值为![]() ;(3)满足条件的点P坐标为(﹣2,0)或(2,6).
;(3)满足条件的点P坐标为(﹣2,0)或(2,6).
【解析】
(1)设直线AD的解析式为y=kx+b,把A、D两点坐标代入,把问题转化为解方程组即可;
(2)因为A、B关于y轴对称,连接AC交y轴于E,此时△BEC的周长最小;
(3)分两种情形分别讨论求解即可解决问题;
.解:(1)设直线AD的解析式为y=kx+b,
把A(﹣2,0),D(0,3)代入y=kx+b,得到![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=![]() x+3.
x+3.
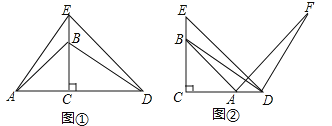
(2)如图1中,∵A(﹣2,0),B(2,0),
∴A、B关于y轴对称,
连接AC交y轴于E,此时△BEC的周长最小,
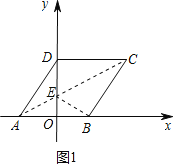
周长的最小值=EB+EC+BC=EA+EC+BC=AC+BC,
∵A(﹣2,0),C(4,3),B(2,0),
∴AC=![]() ,
,
∴△EBC周长的最小值为:![]() .
.
(3)如图2中,
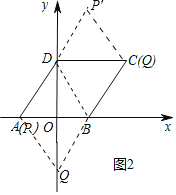
①当点P与A重合时,四边形DPQB是菱形,此时P(﹣2,0),
②当点P′在AD的延长线上时,DP′=AD,此时四边形BDP′Q是菱形,此时P′(2,6).
综上所述,满足条件的点P坐标为(﹣2,0)或(2,6);

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目