题目内容
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 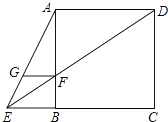
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴ ![]() ,
,
∵AB∥CD,
∴ ![]() ,
,
∵AD=CD,
∴GF=BF
(2)证明:延长GF交AM于H,
∵GF∥BC,
∴FH∥BC,
∴ ![]() ,
,
∴ ![]() ,
,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴FOED=ODEF
【解析】(1)根据已知条件可得到GF∥AD,则有 ![]() ,由BF∥CD可得到
,由BF∥CD可得到 ![]() ,又因为AD=CD,可得到GF=FB;(2)延长GF交AM于H,根据平行线分线段成比例定理得到
,又因为AD=CD,可得到GF=FB;(2)延长GF交AM于H,根据平行线分线段成比例定理得到 ![]() ,由于BM=BE,得到GF=FH,由GF∥AD,得到
,由于BM=BE,得到GF=FH,由GF∥AD,得到 ![]() ,等量代换得到
,等量代换得到 ![]() ,即
,即 ![]() ,于是得到结论.
,于是得到结论.

练习册系列答案
相关题目
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?





