题目内容
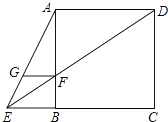
【题目】如图,已知点M、N分别为ABCD的边CD、AB的中点,连接AM、CN. 
(1)证明:AM=CN;
(2)过点B作BH⊥AM于点H,交CN于点E,连接CH,判断线段CB、CH的数量关系,并说明理由. 
【答案】
(1)AM∥NC,
理由:∵点M、N分别为ABCD的边CD、AB的中点,
∴AB=CD,MC=AN,AB∥CD,
∴AN∥MC,AN=MC,
∴四边形ANCM是平行四边形,
∴AM∥NC
(2)解:BC=HC,
理由:∵AM∥NC,AN=BN,
∴BE=HE,
∵BH⊥AM,
∴EB⊥NE,
∴NC垂直平分HB,
∴HC=BC
【解析】(1)利用平行四边形的性质得出AN∥MC,AN=CM,进而利用平行四边形的判定得出答案;(2)利用三角形中位线定理的推论得出HE=EB,以及利用平行线的性质得出NC⊥HB,再利用线段垂直平分线的性质得出答案.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目