题目内容
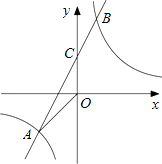
【题目】已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= ![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C. 
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)结合图象直接写出不等式kx+b< ![]() 的解集.
的解集.
【答案】
(1)解:∵B点(1,4)在反比例函数y= ![]() 的图象上,
的图象上,
∴m=1×4=4,
∴反比例函数解析式为y= ![]() ,
,
∵A点(n,﹣2)在反比例函数图象上,
∴n=﹣2,即A点坐标为(﹣2,﹣2),
又∵A、B两点在一次函数图象上,
∴代入一次函数解析式y=kx+b可得
![]() ,
,
解得 ![]() .
.
∴一次函数解析式为y=2x+2
(2)解:在y=2x+2中,令x=0可得y=2,
∴C点坐标为(0,2),
∴OC=2,
又∵A为(﹣2,﹣2),
∴A到OC的距离为2,
∴S△AOC= ![]() ×2×2=2
×2×2=2
(3)解:∵由一次函数与反比例函数的图象可知,当x<﹣2或0<x<1时反比例函数的图象在一次函数图象的上方,
∴当x<﹣2或0<x<1时,反比例函数的值大于一次函数的值,
即不等式kx+b< ![]() 的解集是x<﹣2或0<x<1.
的解集是x<﹣2或0<x<1.
【解析】(1)把B点坐标代入反比例函数解析式可求得反比例函数解析式,则可求得A点坐标,再由A、B两点坐标可求得一次函数解析式;(2)根据一次函数解析式可求得C点的坐标,则可求得OC的长度,且根据A点的坐标可求得A到OC的距离,可求得△AOC的面积;(3)根据两函数图象的交点即可求出反比例函数的值大于一次函数的值时x的取值范围.

 阅读快车系列答案
阅读快车系列答案【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
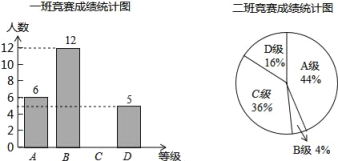
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
一班 | a | b | 90 | 106.24 |
二班 | 87.6 | 80 | c | 138.24 |
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.