题目内容
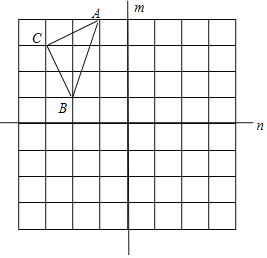
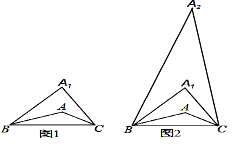
【题目】在△ABC中,∠A=160°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1,则∠A1的度数为__;第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行___步.
【答案】 140° 7
【解析】(1)根据三角形内角和定理和角平分线定义可得∠A1BC+∠A1CB=2(180°-∠A)= 2(180°-160°),故可以求∠A1;
(2)设进行n次,由(1)可得
∠AnBC+∠AnCB=2(180°-∠A)= (n+1)(180°-160°)< 180°.
(1)由已知可得∠A1BC+∠A1CB=2(180°-∠A)= 2(180°-160°)=40°.
∠A1=180°-(∠A1BC+∠A1CB)=140°;
(2)设进行n次,由(1)可得
∠AnBC+∠AnCB=2(180°-∠A)= (n+1)(180°-160°)< 180°
所以,n<8
所以,n的最大值是7.
故答案为:(1). 140° (2). 7

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
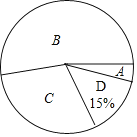
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.