Question

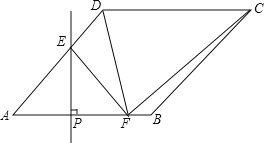
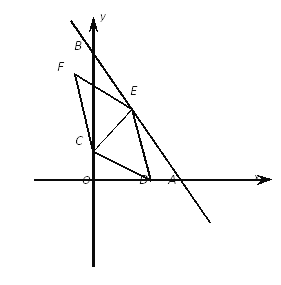
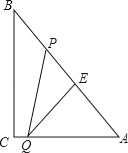
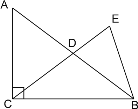
【题目】已知：如图，在Rt△ABC中，∠ACB=90°，D是边AB的中点，CE=CB，CD=5，.

求：（1）BC的长．

（2）tanE的值．

Answer 1

【答案】（1）BC =8; （2）tanE=3.

【解析】

（1）先利用直角三角形斜边的性质求出AC，再利用即可求出AB。再利用勾股定理即可求出BC的长；（2）作EH⊥BC垂足为，求得△EHC∽△ACB，利用相似三角形的性质求出EH,CH，BH，再利用三角函数的定义即可求解.

（1） ∵在Rt△ABC中，∠ACB=90°，是边的中点;

∴,

∵;∴;

∵sin∠ABC=;

由解得;

∵ ∴.

（2）作EH⊥BC垂足为；

∴；

∵D是边AB的中点；

∴BD=CD=AB； ∴∠DCB=∠ABC;

∵∠ACB=90°； ∴∠EHC=∠ACB ； ∴△EHC∽△ACB

∴；

由BC=8，CE=CB,得CE=8，∠CBE=∠CEB，；

∴解得EH=,CH=；;

∴，即tanE=3.