��Ŀ����
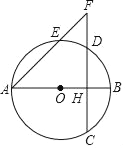
����Ŀ����ͼ��Rt��ABC�У���C��90�㣬BC��8cm��AC��6cm����P��B������BA��A�˶����ٶ�Ϊÿ��1cm����E�ǵ�B��PΪ�Գ����ĵĶԳƵ㣬��P�˶���ͬʱ����Q��A������AC��C�˶����ٶ�Ϊÿ��2cm������Q���ﶥ��Cʱ��P��Qͬʱֹͣ�˶�����P��Q�����˶�ʱ��Ϊt�룮
(1)��tΪ��ֵʱ��PQ��BC��
(2)���ı���PQCB�����Ϊy����y����t�ĺ�����ϵʽ��
(3)�ı���PQCB����ܷ��ǡ�ABC�����![]() �����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
�����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
(4)��tΪ��ֵʱ����AEQΪ���������Σ���ֱ��д�������
���𰸡�(1)t��![]() ��(2)y��
��(2)y��![]() t2��8t+24��(3)�ı���PQCB������ǡ�ABC�����
t2��8t+24��(3)�ı���PQCB������ǡ�ABC�����![]() ����ʱt��ֵΪ5��
����ʱt��ֵΪ5��![]() ��(4)��tΪ
��(4)��tΪ![]() ��
��![]() ��
��![]() ��ʱ����AEQΪ���������Σ�
��ʱ����AEQΪ���������Σ�
��������
���⣨1������Rt��ABC�У��ɹ��ɶ������AB=10������BP=t��AQ=2t���ó�AP=10-t��Ȼ����PQ��BC������ƽ���߷��߶γɱ��������ó�![]() ���г�����ʽ
���г�����ʽ![]() ����⼴�ɣ�
����⼴�ɣ�
��2������S�ı���PQCB=S��ACB-S��APQ=![]() ACBC-
ACBC-![]() APAQsinA�����ɵó�y����t�ĺ�����ϵʽ��
APAQsinA�����ɵó�y����t�ĺ�����ϵʽ��
��3�������ı���PQCB�������ABC�����![]() ���г�����
�������![]() t2-8t+24=
t2-8t+24=![]() ��24���ⷽ�̼��ɣ�
��24���ⷽ�̼��ɣ�
��4����AEQΪ����������ʱ��������������ۣ���AE=AQ����EA=EQ����QA=QE��ÿһ������������г�����t�ķ��̣��ⷽ�̼��ɣ�
�����������1��Rt��ABC�У��ߡ�C=90����BC=8cm��AC=6cm��
��AB=10cm��
��BP=t��AQ=2t��
��AP=AB-BP=10-t��
��PQ��BC��
��![]() ��
��
��![]() ��
��
���t=![]() ��
��
��2����S�ı���PQCB=S��ACB-S��APQ=![]() ACBC-
ACBC-![]() APAQsinA
APAQsinA
��y=![]() ��6��8-
��6��8-![]() ����10-2t��2t
����10-2t��2t![]() =24-
=24-![]() t��10-2t��=
t��10-2t��=![]() t2-8t+24��
t2-8t+24��
��y����t�ĺ�����ϵʽΪy=![]() t2-8t+24��
t2-8t+24��
��3���ı���PQCB���������ABC�����![]() ���������£�
���������£�
�����⣬��
![]() t2-8t+24=
t2-8t+24=![]() ��24��
��24��
��������t2-10t+12=0��
���t1=5-![]() ��t2=5+
��t2=5+![]() ������������ȥ����
������������ȥ����
���ı���PQCB���������ABC�����![]() ����ʱt��ֵΪ5-
����ʱt��ֵΪ5-![]() ��
��
��4����AEQΪ����������ʱ��������������ۣ�
�����AE=AQ����ô10-2t=2t�����t=![]() ��
��
�����EA=EQ����ô��10-2t����![]() =t�����t=
=t�����t=![]() ��
��
�����QA=QE����ô2t��![]() =5-t�����t=
=5-t�����t=![]() ��
��
�ʵ�tΪ![]() �롢
�롢![]() �롢
�롢![]() ��ʱ����AEQΪ���������Σ�
��ʱ����AEQΪ���������Σ�

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�