题目内容
【题目】![]() 尝试探究
尝试探究
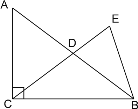
如图-![]() ,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
![]()
![]() 的值为 ;
的值为 ;![]() 直线
直线![]() 与直线
与直线![]() 的位置关系为 ;
的位置关系为 ;
![]() 类比延伸
类比延伸
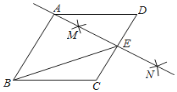
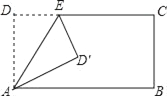
如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直
与直![]() 线的位置关系,并说明理由;
线的位置关系,并说明理由;
![]() 拓展运用
拓展运用
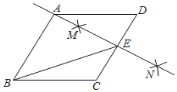
若![]() ,在旋转过程中,当
,在旋转过程中,当![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
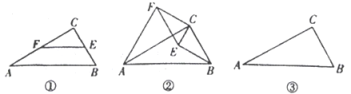
【答案】![]()
![]()
![]() ;
;![]()
![]() ;
;![]()
![]()
![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)①根据直角三角形30°角的性质即可解决问题;
②根据已知可直接得出答案;
(2)只要证明△ACF△BCE,根据相似三角形的性质即可得![]() 的值,也可得∠BCE=∠CAF,继而推导
的值,也可得∠BCE=∠CAF,继而推导![]() 即可得;
即可得;
(3)分两种情况画出图形分别解决即可.
![]() ①∵在△ABC中,∠ABC=90°,∠A=30°,EF//AB,
①∵在△ABC中,∠ABC=90°,∠A=30°,EF//AB,
∴∠CFE=∠A=30°,
∴CF=![]() =
=![]() EC,AC=
EC,AC=![]() =
=![]() BC,
BC,
∴AF=AC-CF=![]() BC-
BC-![]() EC=
EC=![]() (BC-EC)=
(BC-EC)=![]() BE,
BE,
∴![]() =
=![]() ,
,
故答案为:![]() ;
;
②∵∠ACB=90°,
∴![]() ,即直线
,即直线![]() 与直线
与直线![]() 的位置关系为垂直,
的位置关系为垂直,
故答案为:![]() ;
;
![]()
![]()
![]() ,
,
理由如下:由![]() 及旋转的性质知
及旋转的性质知![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,
,
∴![]() =
=![]()
![]() ,
,
![]() ,
,
如图,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
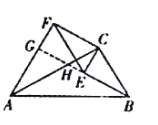
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() ;
;
![]() ①如图,∵△ECB∽△FCA,∴AF:BE=CF:CE=
①如图,∵△ECB∽△FCA,∴AF:BE=CF:CE=![]() ,
,
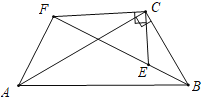
设BE=a,则AF=![]() a,
a,
∵B、E、F共线,∴∠BEC=∠AFC=120°,
∵∠EFC=30°,∴∠AFB=90°,
在Rt△ABF中,AB=2BC=6,AF=![]() a,BF=EF+BE=4+a,
a,BF=EF+BE=4+a,
∴![]() ,
,
∴a=-1+![]() 或-1-
或-1-![]() (舍去),
(舍去),
∴AF=![]() a=
a=![]() ;
;
②如图,当E、B、F共线时,同法可证:AF=![]() BE,∠AFB=90°,
BE,∠AFB=90°,
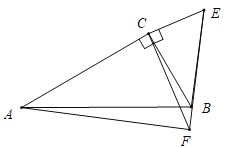
在Rt△ABF中,![]() ,
,
∴a=1+![]() 或1-
或1-![]() (舍去),
(舍去),
∴AF=![]() a=
a=![]() ,
,
综上,AF的长为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目