题目内容
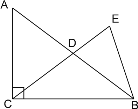
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE =________.

【答案】![]() (或4.8)
(或4.8)
【解析】
过D作DG⊥BC于G,依据折叠的性质即可得到CD垂直平分BE,再根据AE∥CD,得出CD=BD=2.5,进而得到BG=1.5,再根据![]() BC×DG=
BC×DG=![]() CD×BF,即可得到BF的长,即可得出BE的长.
CD×BF,即可得到BF的长,即可得出BE的长.
解:如图所示,过D作DG⊥BC于G,
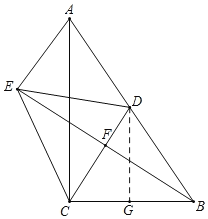
由折叠可得,CD垂直平分BE,
∴当CD∥AE时,∠AEB=∠DFB=90°,
∴∠DEB+∠DEA=90°,∠DBE+∠DAE=90°,
∵DB=DE,
∴∠DEB=∠DBE,
∴∠DAE=∠DEA,
∴AD=DE,
∴AD=BD,
∴D是AB的中点,
∴Rt△ABC中,CD=BD=2.5,
∵DG⊥BC,
∴BG=1.5,
∴Rt△BDG中,DG=2,
∵![]() BC×DG=
BC×DG=![]() CD×BF,
CD×BF,
∴BF=![]() =
=![]() ,
,
∴BE=2BF=![]() ,
,
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目