Question

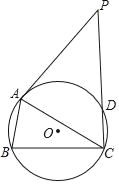
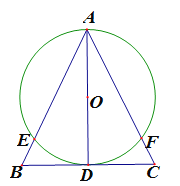
【题目】如图，△ABC中，AB=AC，AD⊥BC于D，以AD为直径的⊙O交AB于E，交AC于F．

（1）求证：BE=CF；

（2）若AE=4，BC=，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接DE、DF，根据等腰三角形的“三线合一”性质可知∠BAD＝∠CAD，BD＝CD，由直径所对的圆周角是直角可知：∠AED＝∠AFD＝90°，进而证得△ADE≌△ADF，根据全等三角形的性质可得AE＝AF，继而可得BE＝CF；

（2）由题意得：∠ADB＝90°,则∠B＋∠BAD＝90°由直径所对的圆周角是直角可知：∠BED＝∠AED＝90°，进而可得∠B＋∠BDE＝90°,根据等量代换可得∠BAD＝∠BDE，进而可证△ABD∽△DBE，设BE＝x，根据相似三角形的性质可得关于x的方程，解方程可得x的值，再根据勾股定理可求出AD，进而可得⊙O的半径．

（1）连接DE、DF，

∵AB=AC，AD⊥BC于D

∴∠BAD＝∠CAD，BD＝CD，

∵AD为⊙O的直径，

∴∠AED＝∠AFD＝90°，

∴DE＝DF，

∵∠ADE＝180°－∠AED－∠EAD

∠ADF＝180°－AFD－∠FAD

∴∠ADE＝∠ADF

又∵AD＝AD

∴△ADE≌△ADF（ASA），

∴AE＝AF

∴AB－AE＝AC－AF

∴BE＝CF

（2）∵AD⊥BC于D

∴∠ADB＝90°,

∴∠B＋∠BAD＝90°

∵直径所对的圆周角是直角

∴∠BED＝∠AED＝90°，

∴∠B＋∠BDE＝90°,

根据等量代换可得∠BAD＝∠BDE，

∴△ABD∽△DBE，

∴＝

即

设BE＝x，

∵AE=4，BC=

∴BD＝BC＝

∴5＝（4＋x）x

解得：x1＝1，x2＝﹣5（舍去）

∴BE＝1，AB＝1＋4＝5，

由勾股定理可得：

AD＝＝＝

∴OD＝OA＝，

即⊙O的半径为．