题目内容
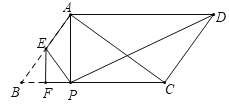
【题目】如图,在平行四边形![]() 中,
中,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
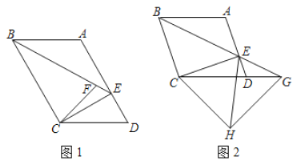
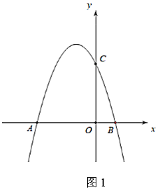
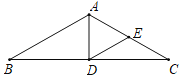
(1)如图1,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
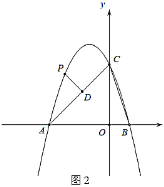
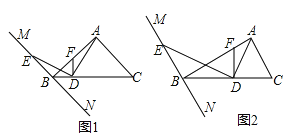
(2)如图2,若![]() ,延长
,延长![]() 交
交![]() 延长线于点
延长线于点![]() ,以
,以![]() 为斜边做等腰直角
为斜边做等腰直角![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)EF=![]() ﹣4;(2)见详解
﹣4;(2)见详解
【解析】
(1)先利用勾股定理得出CE=![]() ,然后在Rt△BCE中,依据勾股定理可得
,然后在Rt△BCE中,依据勾股定理可得![]() ,进而得出EF=
,进而得出EF=![]() ﹣4;
﹣4;
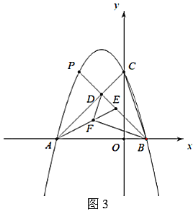
(2)过C作CM⊥CG,交GH的延长线于M,连接EM,判定△BCG≌△ECM(SAS),即可得出∠CEM=∠CBG=45°,再根据H是MG的中点,即可得到Rt△MEG中,EH=![]() MG=HG.
MG=HG.
解:(1)∵平行四边形ABCD中,CE⊥BC,
∴CE⊥AD,
又∵∠ECD=30°,
∴Rt△CDE中,DE=![]() CD=1,
CD=1,
∴![]()
又∵在Rt△BCE中,BC=4,
∴![]() ,
,
∴EF=BE﹣BF=![]() ﹣4;
﹣4;
(2)如图2所示,过C作CM⊥CG,交GH的延长线于M,连接EM,
∵△CGH是等腰直角三角形,∠MCG=90°,
∴∠CGH=∠CMG=45°,
∴CG=CM,
∵∠BCE=90°,∠MCG=90°,
∴∠BCG=∠ECM,
又∵BC=EC,
∴△BCG≌△ECM(SAS),
∴∠CEM=∠CBG=45°,
又∵∠BEC=45°,
∴∠MEG=90°,
又∵CM=CG,CH平分∠MCG,
∴H是MG的中点,
∴Rt△MEG中,EH=![]() MG=HG.
MG=HG.


练习册系列答案
相关题目