ÌâÄżÄÚÈĘ
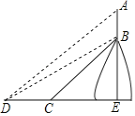
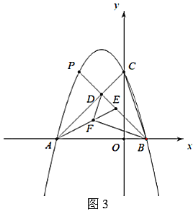
ĄŸÌâÄżĄżÎ»ÓÚÖŰÇìÊл㱱Çű”ÄŐŐĞɜÉÁÖč«Ô°łËłĐĄ°œüŚÔÈ»Ą±ÉúÌŹÀíÄîÓȘÔìÉÁַ矰ŁŹĄ°ËäÓÉÈËŚśŁŹÍđŚÔÌìżȘĄ±ŁŹÍčÏÔŚÔÈ»·çčÇÓëÔÉúÒ°È€ŁźÉœÖĐŚîÎȘÖőÄż”ÄŸ”ä”±ÊôÀżĐÇËțŁź”ÇÁÙËț¶„ŁŹżÉÉÏŸĆÌìŃûÔÂÀżĐÇŁŹżÉÄńî«ĐÂÇűŁŹÁìÂÔžœœü„Óî”ÄŚłĂÀŁ»ÒàżÉÔ¶ÌśÁœœÊ€Ÿ°Łź”ÇÁÙŽËËțŁŹÈĂÄăÓĐÆźÈ»ÈôÏÉ”ÄÁȘÏëÓÖÓДǞßÔ¶ÌśŁŹĄ°Ò»ÀÀÖÚÉœĐĄĄ±”ÄŐđșłŁŹÎÒĐŁÄłÊęѧĐËÈ€ĐĄŚé”Ä͏ѧŚŒ±žÀûÓĂËùѧ”ÄÈęœÇșŻÊęÖȘʶčÀČâžĂËț”Äžß¶ÈŁŹÒŃÖȘÀżĐÇËțABλÓÚƶÈlŁœ![]() :1”ÄбÆÂBCÉÏŁŹČâÁżÔ±ŽÓбÆ”Ś¶ËCŽŠÍùÇ°ŃŰËźÆœ·œÏòŚßÁË120mŽï”œ”ŰĂæDŽŠŁŹŽËʱČâ”ĂÀżĐÇËțAB¶„¶ËA”ÄŃöœÇÎȘ37ĄăŁŹÀżĐÇËț”Ś¶ËB”ÄŃöœÇÎȘ30ĄăŁŹÒŃÖȘAĄąBĄąCĄąDÔÚÍŹÒ»ÆœĂæÄÚŁŹÔòžĂËțAB”Ğ߶ÈÎȘŁšĄĄĄĄŁ©mŁŹŁšœáčû±ŁÁôŐûÊ꣏ČÎżŒÊęŸĘŁ»sin37ĄăĄÖ0.60ŁŹcos37ĄăĄÖ0.80ŁŹtan37ĄăĄÖ0.75ŁŹ
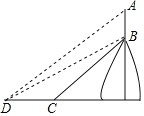
:1”ÄбÆÂBCÉÏŁŹČâÁżÔ±ŽÓбÆ”Ś¶ËCŽŠÍùÇ°ŃŰËźÆœ·œÏòŚßÁË120mŽï”œ”ŰĂæDŽŠŁŹŽËʱČâ”ĂÀżĐÇËțAB¶„¶ËA”ÄŃöœÇÎȘ37ĄăŁŹÀżĐÇËț”Ś¶ËB”ÄŃöœÇÎȘ30ĄăŁŹÒŃÖȘAĄąBĄąCĄąDÔÚÍŹÒ»ÆœĂæÄÚŁŹÔòžĂËțAB”Ğ߶ÈÎȘŁšĄĄĄĄŁ©mŁŹŁšœáčû±ŁÁôŐûÊ꣏ČÎżŒÊęŸĘŁ»sin37ĄăĄÖ0.60ŁŹcos37ĄăĄÖ0.80ŁŹtan37ĄăĄÖ0.75ŁŹ![]() ĄÖ1.73Ł©
ĄÖ1.73Ł©
A.31B.40C.60D.136
ĄŸŽđ°žĄżA
ĄŸœâÎöĄż
ÉèABĄÍDCÓÚEŁŹÉèCEŁœxmŁŹÔòBEŁœ![]() xmŁŹžùŸĘDC=120mżÉÏÈÁĐłö·œłÌÇółöx”ÄÖ”ŁŹŽÓ¶ű”ĂłöBEŁŹDE”Äł€ŁŹÔÚRtĄśADEÖĐżÉÇółöAE”Äł€ŁŹŽÓ¶űÓÉAB=AE-BEżÉ”Ă”œœáÂÛŁź
xmŁŹžùŸĘDC=120mżÉÏÈÁĐłö·œłÌÇółöx”ÄÖ”ŁŹŽÓ¶ű”ĂłöBEŁŹDE”Äł€ŁŹÔÚRtĄśADEÖĐżÉÇółöAE”Äł€ŁŹŽÓ¶űÓÉAB=AE-BEżÉ”Ă”œœáÂÛŁź
œâŁșÈçÍŒŁŹÉèABĄÍDCÓÚEŁŹ
ÉèCEŁœxmŁŹÔòBEŁœ![]() xmŁŹ
xmŁŹ
ÔÚRtĄśBDEÖĐŁŹĄßĄÏBDEŁœ30ĄăŁŹ
ĄàDEŁœ![]() Łœ
Łœ![]() Łœ3xŁŹ
Łœ3xŁŹ
ĄàDCŁœDE©CEŁœ3x©xŁœ120ŁŹ
ĄàxŁœ60ŁŹ
ĄàBEŁœ60![]() mŁŹDEŁœ180mŁŹ
mŁŹDEŁœ180mŁŹ
ÔÚRtĄśADEÖĐŁŹAEŁœDEtan37ĄăĄÖ180ĄÁ0.75Łœ135ŁšmŁ©ŁŹ
ĄàABŁœAE©BEŁœ135©60![]() ĄÖ31(m)ŁŹ
ĄÖ31(m)ŁŹ
čÊŃĄŁșAŁź