题目内容
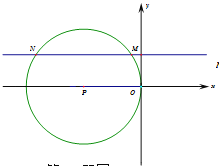
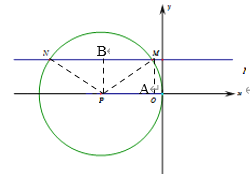
【题目】如图,点P为x轴上一点,M为以P为圆心、PO为半径的圆上一点,过M作MN∥x轴交⊙P于另一点N,若M点的坐标为(-1,3),则点N的坐标为_____.
【答案】(-9,3)
【解析】
连接PM、PN、过点M作MA⊥x轴于点A,过点P作PB⊥MN于点B,设PO=r,则PM=PN=PO=r,由M坐标(﹣1,3)推出OA=1,MA=3,AP=(r-1),由勾股定理可得
![]() ,列关于r的一元二次方程,解方程得r=5,继而得P的坐标为(﹣5,0),根据平行线的性质可得N的纵坐标为3,根据矩形的判定和性质可得MB=AP=4,由垂径定理可得:NB=MB=4,继而推出N的横坐标为﹣9即可.
,列关于r的一元二次方程,解方程得r=5,继而得P的坐标为(﹣5,0),根据平行线的性质可得N的纵坐标为3,根据矩形的判定和性质可得MB=AP=4,由垂径定理可得:NB=MB=4,继而推出N的横坐标为﹣9即可.
连接PM、PN、过点M作MA⊥x轴于点A,过点P作PB⊥MN于点B,设PO=r,则PM=PN=PO=r,
∵M坐标为(﹣1,3)
∴OA=1,MA=3,AP=PO﹣OA=r﹣1
在Rt△MPA中,由勾股定理可得
![]() ,即
,即![]() ,解得r=5,
,解得r=5,
∴圆心P的坐标为(﹣5,0)
∵MN∥x轴交⊙P于另一点N
∴N的纵坐标为3
∵PB⊥MN,MA⊥x轴,MN∥x轴
∴∠PBM=∠PAM=∠AMB=∠MBP=90°
∴四边形APBM是矩形,
∴MB=AP=5-1=4
由垂径定理可得:NB=MB=4
∴N的横坐标为:﹣5-4=﹣9
∴点N的坐标为(﹣9,3)
故答案为:(﹣9,3)

练习册系列答案
相关题目