题目内容
【题目】如图,在正方形ABCD内有一点P,PA=5,PB=![]() ,PC=
,PC=![]() ,将△BPC绕点B逆时针旋转90°.
,将△BPC绕点B逆时针旋转90°.
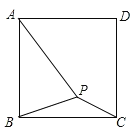
(1)画出旋转后的图形;
(2)求点C和点P′的距离.
【答案】(1)如图所示,△ABP'即为所求;见解析;(2)点C和点P′的距离为3![]() .
.
【解析】
(1)根据旋转的性质将图形进行旋转作图即可解决.
(2)根据旋转的性质和勾股定理求出AP'2+PP'2的值与AP2的值进行比较,然后确定△APP'是直角三角形,然后角角之间的关系求∠CPP'的度数,根据平角的定义得到P',P,C三点共线,最后求CP′的长度即可.
(1)分别将BP、BC绕点B逆时针旋转90°,依次连接即可,如图所示,△ABP'即为所求;
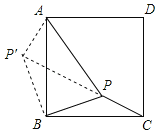
(2)由旋转可得△BCP≌△BAP',
∴AP'=CP=![]() ,BP'=BP=
,BP'=BP=![]() ,∠ABP'=∠CBP,
,∠ABP'=∠CBP,
∵∠ABC=∠ABP+∠CBP=90°,
∴∠PBP'=∠ABP+∠ABP'=90°,
∴Rt△PBP'中,PP'=![]() =2
=2![]() ,∠BP'P=∠BPP'=45°,
,∠BP'P=∠BPP'=45°,
∴AP'2+PP'2=5+20=25,
又∵AP2=25,
∴AP'2+PP'2=AP2,
∴△APP'是直角三角形,且∠AP'P=90°,
∴∠AP'B=135°,
∴∠BPC=135°,
∴∠CPP'=135°+45°=180°,即P',P,C三点共线,
∴CP'=PP'+CP=2![]()
![]() =3
=3![]() ,
,
即点C和点P′的距离为3![]() .
.

 全优点练单元计划系列答案
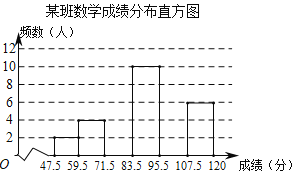
全优点练单元计划系列答案【题目】某市为了解九年级学生数学模拟考试成绩情况,随机抽取部分学生的成绩进行分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 47.5~59.5 | 2 | 0.05 |
2 | 59.5~71.5 | 4 | 0.10 |
3 | 71.5~83.5 | a | 0.2 |
4 | 83.5~95.5 | 10 | 0.25 |
5 | 95.5~107.5 | b | c |
6 | 107.5~120 | 6 | 0.15 |
合计 | d | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ,d= ;
(2)补充完整频数分布直方图.
(3)已知全市九年级共有3500名学生参加考试,成绩96分及以上为优秀,估计全市九年级学生数学模拟考试成绩为优秀的学生人数是多少?