题目内容
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
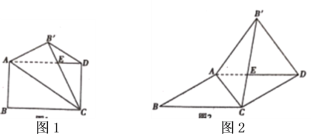
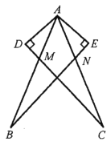
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
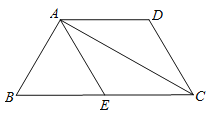
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
【答案】(1)①平行;②菱形; (2)结论①、②都成立,理由详见解析.
【解析】
(1)①由平行线的性质和折叠的性质可得∠DAC=∠ACE,由∠AB'C=∠ADC=90°,可证点A,点C,点D,点B'四点共圆,可得∠ADB'=∠ACE=∠DAC,可得AC∥B'D;②由菱形的定义可求解;
(2)都成立,设点E的对应点为F,由平行线的性质和折叠的性质可得∠DAC=∠ACE,AF=AE,CE=CF,可得AF=AE=CE=CF,可得四边形AECF是菱形.
解:(1)①∵四边形ABCD是矩形
∴AD∥BC,∠B=∠ADC=90°
∴∠DAC=∠ACB
∵将矩形纸片ABCD沿对角线AC翻折,
∴∠AB'C=∠B=90°,∠ACB=∠ACE
∴∠DAC=∠ACE,
∴AE=EC
∵∠AB'C=∠ADC=90°
∴点A,点C,点D,点B'四点共圆,
∴∠ADB'=∠ACE,
∴∠ADB'=∠DAC
∴B'D∥AC,
故答案为:平行
②∵将△AEC剪下后展开,AE=EC
∴展开图形是四边相等的四边形,
∴展开图形是菱形
(2)都成立,
如图2,设点E的对应点为F,
∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠DAC=∠ACB
∵将矩形纸片ABCD沿对角线AC翻折,
∴∠ACB=∠ACE,AF=AE,CE=CF
∴∠DAC=∠ACE,
∴AE=EC
∴AF=AE=CE=CF
![]() 四边形
四边形![]() 是菱形.
是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目