题目内容
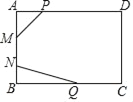
【题目】如图，在矩形ABCD中，
，
，对角线AC，BD交于点
点P从点A出发，沿AD方向匀速运动，速度为
；同时，点Q从点D出发，沿DC方向匀速运动，速度为；当一个点停止运动时，另一个点也停止运动
连接PO并延长，交BC于点E，过点Q作
，交BD于点
设运动时间为
，解答下列问题：
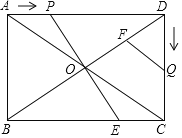
（1）当t为何值时，
是等腰三角形；
（2）设五边形OECQF的面积为
，试确定S与t的函数关系式．
【答案】（1）
或5；（2）
.
【解析】
（1）根据矩形的性质和勾股定理得到AC=10，①当AP=PO=t，过P作PM⊥AO，根据相似三角形的性质得到AP=t=，②当AP=AO=t=5，于是得到结论；
（2）过点O作OH⊥BC交BC于点H，已知BE=PD，则可求△BOE的面积；可证得△DFQ∽△DOC，由相似三角形的面积比可求得△DFQ的面积，从而可求五边形OECQF的面积．
解：（1）在矩形ABCD中，
，
，
，
①当
，
过P作
，
，
，
，
∽
，
，
，
②当
，
当t为或5时，
是等腰三角形；
（2）
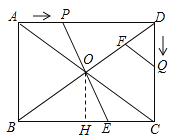
过点O作
交BC于点H，则
．
由矩形的性质可知
，
，又得
，
≌BOE，
，
则
，
∽
，相似比为
，
，
，
，
；
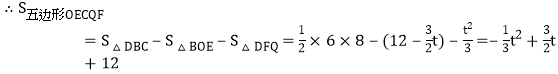与t的函数关系式为
；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
