题目内容
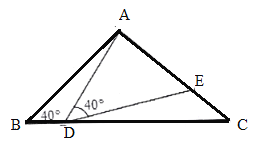
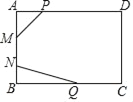
【题目】如图,矩形ABCD中,AB=6,MN在边AB上运动,MN=3,AP=2,BQ=5,PM+MN+NQ最小值是_____.
【答案】![]()
【解析】
作点P关于直线AB的对称点P′,过点P′G⊥BC,交CB的延长线与点G,在P′G上截取P′M′=MN=3,连M′Q交AB于点M,过点P′作P′N∥M′Q交AB于点N,此时PM+MN+NQ的值最小. 根据作法可得PM+MN+NQ= P′M ′+ QM ′,由此求得P′M ′、 QM ′的长即可求解.
如图,作点P关于直线AB的对称点P′,过点P′G⊥BC,交CB的延长线与点G,在P′G上截取P′M′=MN=3,连M′Q交AB于点M,过点P′作P′N∥M′Q交AB于点N,此时PM+MN+NQ的值最小.

∵P′N∥M′Q,P′M ′∥M N,
∴四边形P′M ′MN为平行四边形,
∴P′N= M ′M,P′M ′=MN=3,
由轴对称的性质可得PN= P′N,AP=A P′=2,
∴PM+MN+NQ= P′M ′+ QM ′,
∵AB= P′G=3,P′M ′=3,AP′=GB=2,
∴GM ′= 3,GQ=7,
在Rt△GQM P′中,由勾股定理可得,QM ′=![]() .
.
∴PM+MN+NQ= P′M ′+ QM ′=![]() .
.
故答案为:![]() .
.

【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
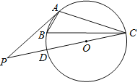
【题目】如图,已知![]() 、
、![]() 分别为
分别为![]() 的直径和弦,
的直径和弦,![]() 为
为![]() 的中点,
的中点,![]() 垂直于
垂直于![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,下列结论一定错误的是( )
,下列结论一定错误的是( )
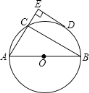
A. DE是⊙O的切线 B. 直径AB长为20cm
C. 弦AC长为16cm D. C为![]() 的中点
的中点
【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.