题目内容
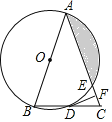
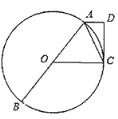
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是弦,
是弦,![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线:
的切线:
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]()
【解析】
(1)过O作OE⊥AC交AC于E,通过![]() ,得到∠ACD=∠COE,最后可得∠DCO=90°;
,得到∠ACD=∠COE,最后可得∠DCO=90°;
(2)由(1)易知∠OAC=∠CAD,所以只需在Rt△ADC中求出cos∠CAD即可.
(1)证明: 过O作OE⊥AC交AC于E,如图所示:
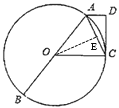
∵OA=OC,OE⊥AC
∴![]()
∵![]()
∴∠ACD=∠COE
∵∠ACO+∠COE=90°
∴∠ACO+∠ACD=90°=∠OCD
∴CD为圆O的切线.
(2)解:由(1)知:∠ACO+∠ACD=90°
∵AD⊥CD
∴∠ACD+∠CAD=90°
∴∠CAD=∠OCA=∠OAC
过A作AF⊥OC,如图示:
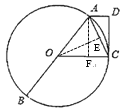
∵AB=10
∴OA=5
∵AD=2
∴OF=3
∴AF=![]() =CD
=CD
∴AC=![]()
∴cos∠DAC=![]() =cos∠OAC
=cos∠OAC

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某校同学组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是![]() 分2,则成绩较为整齐的是 队.
分2,则成绩较为整齐的是 队.