题目内容
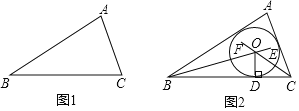
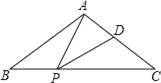
【题目】如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
【答案】(1)证明见解析;(2)BP=![]() .
.
【解析】
(1)由题意可得∠ABC=∠ACB,∠DPC=∠BAP,可证△ABP∽△PCD;
(2))由△ABP∽△PCD,可得![]() ,由PD∥AB,可得
,由PD∥AB,可得![]() ,即
,即![]() ,可求BP的长.
,可求BP的长.
(1)∵AB=AC,∴∠ABC=∠ACB.
∵∠APC=∠ABC+∠BAP,∴∠APD+∠DPC=∠ABC+∠BAP,且∠APD=∠B,∴∠DPC=∠BAP且∠ABC=∠ACB,∴△BAP∽△CPD.
(2)∵△ABP∽△PCD,∴![]() 即
即![]() .
.
∵PD∥AB,∴![]() 即
即![]() ,∴
,∴![]() ,∴
,∴![]() ,∴BP
,∴BP![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目