题目内容
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
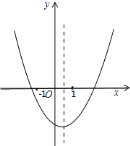
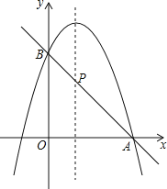
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】(1)、m>﹣1;(2)、P(1,2);(3)、x<0或x>3 .
【解析】
试题分析:(1)、根据图像与x轴有两个交点,则△>0求出m的取值范围;(2)、根据点A坐标得出二次函数的解析式,然后得出点B的坐标,根据待定系数法求出直线AB的解析式,从而得出点P的坐标;(3)、根据图像直接得出答案.
试题解析:(1)、∵二次函数的图象与x轴有两个交点,∴△=22+4m>0 ∴m>﹣1;
(2)、∵二次函数的图象过点A(3, 0), ∴0=﹣9+6+m ∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3, 令x=0,则y=3, ∴B(0,3),
设直线AB的解析式为:y=kx+b, ∴![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为:y=﹣x+3, ∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2, ∴P(1,2).
(3)、x<0或x>3

练习册系列答案
相关题目