题目内容
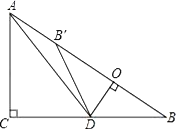
【题目】如图，在△ABC中，∠A＝90°，P是BC上一点，且DB＝DC，过BC上一点P，作PE⊥AB于E，PF⊥DC于F，已知：AD：DB＝1：3，BC＝
，则PE+PF的长是（ ）
A. B. 6C. 
D. 
【答案】C
【解析】
根据三角形的面积判断出PE+PF的长等于AC的长，这样就变成了求AC的长；在Rt△ACD和Rt△ABC中，利用勾股定理表示出AC，解方程就可以得到AD的长，再利用勾股定理就可以求出AC的长，也就是PE+PF的长．
∵△DCB为等腰三角形，PE⊥AB，PF⊥CD，AC⊥BD，
∴S△BCD=
BDPE+CDPF=BDAC，
∴PE+PF=AC，
设AD=x，BD=CD=3x，AB=4x，
∵AC2=CD2-AD2=（3x）2-x2=8x2，
∵AC2=BC2-AB2=（
）2-（4x）2，
∴x=2，
∴AC=4
，
∴PE+PF=4．
故选：C
阅读快车系列答案
【题目】据调查，初中学生课桌椅不合格率达76.7%（不合格是指不能按照学生不同的身高来调节课桌椅的高度），为了解初中生的身高情况，随机抽取了某校初中部分男生、女生进行调查收集数据如下：
男生身高（单位：cm）：163 161 160 163 161 162 163 164 163 163
女生身高（单位：cm）：164 161 160 161 161 162 160 162 163 162
整理数据：
160 | 161 | 162 | 163 | 164 | |
男生（人） | 1 | 2 | 1 | a | 1 |
女生（人） | 2 | b | 3 | 1 | 1 |
根据以上信息，解答下列问题：
（1）填空：a＝ ，b＝ ，并补全条形统计图；
（2）现有两名身高都为163cm的男生和女生，比较这两名同学分别在男生、女生中的身高情况，并简述理由；
（3）根据相关研究发现，只有身高为161cm的初中生课桌椅是合格的，试估计全校1000名学生中，有多少名学生的课桌椅是合格的？
