题目内容
【题目】如图，在同一平面内，两条平行高速公路l1和l2间有一条“Z”型道路连通，其中AB段与高速公路l1成30°角，长为20km；BC段与AB、CD段都垂直，长为10km，CD段长为30km，求两高速公路间的距离（结果保留根号）．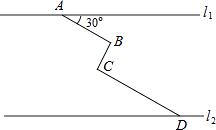 
【答案】解：过B点作BE⊥l1 ， 交l1于E，CD于F，l2于G．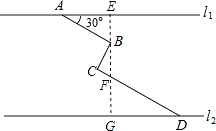 
在Rt△ABE中，BE=ABsin30°=20× 
=10km，
在Rt△BCF中，BF=BC÷cos30°=10÷ 
= 
km，
CF=BFsin30°= × = 
km，
DF=CD﹣CF=（30﹣ ）km，
在Rt△DFG中，FG=DFsin30°=（30﹣ ）× =（15﹣ 
）km，
∴EG=BE+BF+FG=（25+5 
）km．
故两高速公路间的距离为（25+5 ）km．
【解析】过B点作BE⊥l1 ， 交l1于E，CD于F，l2于G．在Rt△ABE中，根据三角函数求得BE，在Rt△BCF中，根据三角函数求得BF，在Rt△DFG中，根据三角函数求得FG，再根据EG=BE+BF+FG即可求解．
练习册系列答案
相关题目
【题目】为了深化课程改革，省实验积极开展校本课程建设，计划成立“增量阅读”、“趣味数学”、“音乐舞蹈”和“戏剧英语”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了初中部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：
选择意向 | 增量阅读 | 趣味数学 | 音乐舞蹈 | 戏曲英语 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
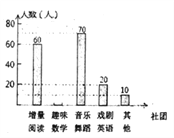
根据统计图表的信息，解答下列问题：
(l)求本次抽样调查的学生总人数及a、b的值：
(2)将条形统计图补充完整；
(3)若该校共有5000名学生，试估计全校选择“音乐舞蹈”社团的学生人数．