题目内容
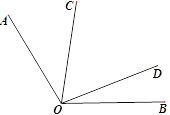
【题目】如图,已知∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,下列说法:
①如果∠AOC=∠BOD,则图中有两对互补的角;
②如果作OE平分∠BOC,则∠AOC=2∠DOE;
③如果作OM平分∠AOC,且∠MON=90°,则ON平分∠BOD;
④如果在∠AOB外部分别作∠AOC、∠BOD的余角∠AOP、∠BOQ,则![]() ,
,
其中正确的有( )个.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】(1)∵∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,
∴∠AOC+∠BOD=120°-60°=60°,
又∵∠AOC=∠BOD,
∴∠AOC=∠BOD=30°,
∴∠AOD=∠BOC=30°+60°=90°,
∴∠AOD+∠BOC=180°,
又∵∠AOB+∠COD=180°,
∴图中此时有两对互补的角;故①正确;
(2)∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=
∠BOC=![]() (120°-∠AOC),
(120°-∠AOC),
∴∠DOE=![]() (120°-∠AOC)-∠BOD,
(120°-∠AOC)-∠BOD,
又∵∠BOD=120°-60°-∠AOC=60°-∠AOC,
∴∠DOE=![]() (120°-∠AOC)-∠BOD=
(120°-∠AOC)-∠BOD=![]() ∠AOC,
∠AOC,
∴∠AOC=2∠DOE;故②正确;

(3)如图,当ON在∠AOB的外部时,ON不可能平分∠BOD ,故③错误;

(4)∵∠AOP与∠AOC互余,∠BOQ与∠BOD互余,
∴∠AOP=90°-∠AOC,∠BOQ=90°-∠BOD,
∴∠AOP+∠BOD=180°-(∠AOC+∠BOD),
又∵∠AOC+∠BOD=120°-60°=60°,
∴∠AOP+∠BOD=180°-(∠AOC+∠BOD)=120°,
又∵∠COD=60°,
∴![]() .故④正确;
.故④正确;

综上所述,正确的说法是①②④,共3个.
故选C.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目