题目内容
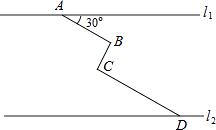
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA’(点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应)如图1

(1)若翻折后A’C=2,则翻折前线段AP= ;
(2)若点P在线段BC上运动,点M为线段A’C的中点,求线段PM的长度;
(3)若点P 在线段BC上运动,点N为B’P的中点,点M为线段A’C的中点,设AP=x,用x表示A’M+PN.
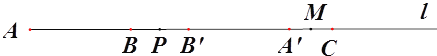
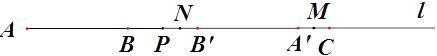
【答案】(1) 11 ;(2) PM=12 ;(3)  .
.
【解析】试题分析:
(1)如图1,由题意可知:AA′=AB+BC-A′C=22,由AP=A′P可得AP=11;
(2)如图3当点A′在点C的左侧时,由(1)可得此时AA′=22,结合已知易得此时:PM=PA′+A′M= ![]() =
= ![]() =
=![]() =12;如图4,当点A′在点C的右侧时,同理可得:PM=PA′-A′M=
=12;如图4,当点A′在点C的右侧时,同理可得:PM=PA′-A′M= ![]() =
=![]() =
= ![]() =12 ;由此即可得到PM=12;
=12 ;由此即可得到PM=12;
(3)根据题意分:①当8<x<12;②当x>12两种情况结合图5、图6分析解答即可.
试题解析:
(1)如图1,当翻折后点A′在点C的左侧时,∵AB=8,BC=16,A′C=2,
∴AA′=AB+BC-A′C=22,
又∵由折叠的性质可知:AP=A′P,
∴AP=11;

(2)①当A′在点C的左侧时,如图3,

由题知PA=PA′,
∵M为AC中点,
∴MA′=MC,
∴PM=PA′+A′M= ![]() =
= ![]() =
=![]() =12;
=12;
②当A′在点C的右侧时,如图4,

∵M为A′C中点,
∴MA′=MC,
∴PM=PA′-A′M= ![]() =
=![]() =
= ![]() =12 ;
=12 ;
综上可得:PM=12 ;
(3)①当8<x<12 此时,A′在C的左侧,如图5,

PB′=PB=x-8,
∵N为BP中点,
∴![]() ,
,
∵A′C=24-2x,
∵M为A′C中点,
∴![]() ,
,
∴![]()
![]() ;
;
②当x>12 ,此时,A′在C的右侧,如图6

PB′=PB=x-8, ![]() ,
,
A′C=2x-24,
∵M为A′C中点,
∴![]() ,
,
∴![]()
![]() ;
;
③当x>24时,如图7,点P不在线段BC上了,不予考虑,
![]()
∴综上所述:  .
.