题目内容
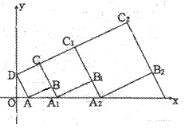
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为_____________
【答案】![]()
【解析】因为点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,
设正方形的面积分别为![]() ,
,![]() …
…![]() ,
,
根据题意,得:AD∥BC∥![]() ∥
∥![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
在直角△ADO中,根据勾股定理,得:AD=![]() ,
,
∴AB=AD=BC=![]() ,
,
∴![]() =5,
=5,
∵∠DAO+∠ADO=90°,∠DAO+![]() =90°,
=90°,
∴∠ADO=![]() ,
,
∴tan![]() =
=![]() ,
,
∴![]() ,
,
∴![]() =BC+
=BC+ ![]() =
=![]() ,
,
∴![]() =
=![]() ×5=5×
×5=5×![]() ,
,
∴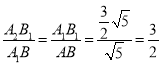 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() S3=8116×5=5×(32)4,
S3=8116×5=5×(32)4,
由此可得: ![]() ,
,
∴![]() .
.
故选:D.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目