题目内容
随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,如图①所示;种植花卉的利润y2与投资量x成二次函数关系,如图②所示(注:利润与投资量的单位:万元)
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润,他能获取的最大利润是多少?
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润,他能获取的最大利润是多少?

(1)设y1=kx,由图①所示,函数y1=kx的图象过(1,2),
所以2=k•1,k=2,
故利润y1关于投资量x的函数关系式是y1=2x(x≥0);
∵该抛物线的顶点是原点,
∴设y2=ax2,
由图②所示,函数y2=ax2的图象过(2,2),
∴2=a•22,a=
,
故利润y2关于投资量x的函数关系式是:y=
x2(x≥0);
(2)设这位专业户投入种植花卉x万元(0≤x≤8),则投入种植树木(8-x)万元,他获得的利润是z万元,根据题意,
得z=2(8-x)+
x2=
x2-2x+16=
(x-2)2+14,
当x=2时,z的最小值是14,
∵0≤x≤8,
∴-2≤x-2≤6,
∴(x-2)2≤36,
∴
(x-2)2≤18,
∴
(x-2)2+14≤18+14=32,
即z≤32,此时x=8,
答:当x=8时,z的最大值是32.
所以2=k•1,k=2,
故利润y1关于投资量x的函数关系式是y1=2x(x≥0);
∵该抛物线的顶点是原点,
∴设y2=ax2,
由图②所示,函数y2=ax2的图象过(2,2),
∴2=a•22,a=
| 1 |
| 2 |
故利润y2关于投资量x的函数关系式是:y=
| 1 |
| 2 |
(2)设这位专业户投入种植花卉x万元(0≤x≤8),则投入种植树木(8-x)万元,他获得的利润是z万元,根据题意,
得z=2(8-x)+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x=2时,z的最小值是14,
∵0≤x≤8,
∴-2≤x-2≤6,
∴(x-2)2≤36,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
即z≤32,此时x=8,
答:当x=8时,z的最大值是32.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

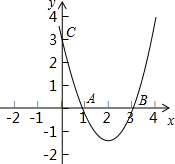
 点,与y轴交于C点,且A、C坐标为(2,0)、(0,3).
点,与y轴交于C点,且A、C坐标为(2,0)、(0,3).
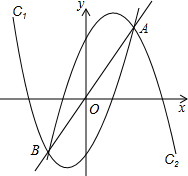 过C2顶点M的直线为l,且l与x轴交于点N.
过C2顶点M的直线为l,且l与x轴交于点N. x2)且(x1+1)(x2+1)=5
x2)且(x1+1)(x2+1)=5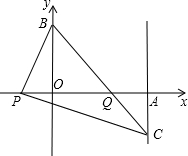 接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)
接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)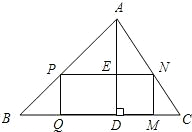 下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.
下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.