题目内容
【题目】几何计算
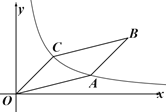
(1)如图1,∠AOC,∠BOD都是直角,且∠AOB与∠AOD的度数比是2:11,求∠BOC的度数.
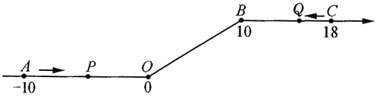
(2)如图2,点C分线段AB为3:4,AC<BC,点D分线段为AB上一点且11BD=3AD,若CD=10cm,求AB的长.

【答案】(1)70°;(2)28cm.
【解析】
(1)设∠AOB=2x°,∠AOD=11x°,根据∠AOD﹣∠AOB=90°得出方程11x﹣2x=90°,求出即可;
(2)先用AB表示出AC及AD的长,再根据CD=10cm可得出AB的长.
解:(1)设∠AOB=2x,则∠AOD=11x,
∵∠DOB=∠AOD﹣∠AOB=9x=90°,
∴x=10°,
∵∠COD+∠BOC=∠AOB+∠BOC=90°,
∴∠COD=2x=20°,
∴∠BOC=7x=70°;
(2)设AD=11xcm,则BD=3xcm,
∴AB=14xcm,
∵AC:CB=3:4,
∴AC=6x,CB=8x,
∴CD=8x﹣3x=5x,
∵CD=10cm,
∴x=2,
∴AB=14x=28.

练习册系列答案
相关题目