题目内容
【题目】感知:如图①,∠C=∠ABD=∠E=90°,可知△ACB∽△BED.(不要求证明)
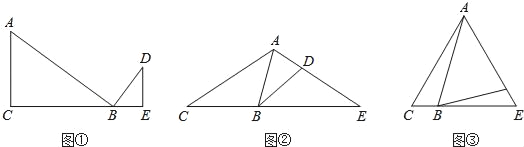
拓展:如图②,∠C=∠ABD=∠E.求证:△ACB∽△BED.
应用:如图③,∠C=∠ABD=∠E=60°,AC=4,BC=1,则△ABD与△BDE的面积比为
.
【答案】拓展:见解析;应用: 13:3;
【解析】试题分析:拓展:由∠C=∠ABD=∠E与∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,即可求得∠CAB=∠DBE,即可证得:△ACB∽△BED.
应用:由△ACB∽△BED,根据相似三角形的对应边成比例,可求得△ABC与△BDE的面积比,△ABC与△ABE的面积比,继而求得答案.
拓展:证明:∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,∠C=∠ABD,
∴∠CAB=∠DBE,
∵∠C=∠E,
∴△ACB∽△BED;
应用:解:∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,∠C=∠ABD,
∴∠CAB=∠DBE,
∵∠C=∠E=60°,
∴△ACB∽△BED,△ACE是等边三角形,
∴AE=AC=4,
∴BE=CE﹣BC=3,
∴△ACB与△BED的相似比为:4:3,
∴S△ABC:S△BED=16:9,S△ABC:S△ABE=1:3=16:48,
设S△ABC=16x,则S△ABE=48x,S△BDE=9x
∴S△ABD=S△ABE﹣S△BED=48x﹣9x=39x,
∴S△ABD:S△BDE=39:9=13:3.
故答案为:13:3.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目