题目内容
如图,在菱形ABCD中,AC=8cm,BD=6,E为CD边中点,点E到BD的距离等于
OC,点P从点A开始沿AC方向以每秒2cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒,当点P在线段AO上运动时,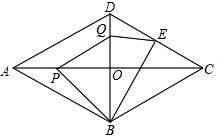
①请用含x的代数式表示OP的长度;
②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);
③是否存在时刻x,四边形PBEQ的面积为13?若存在,求出满足条件的x的值;若不能,请说明理由.
| 1 | 2 |

①请用含x的代数式表示OP的长度;
②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);
③是否存在时刻x,四边形PBEQ的面积为13?若存在,求出满足条件的x的值;若不能,请说明理由.
分析:①根据菱形的性质得出AO,BO的长,再利用P点运动速度得出OP的长即可;
②根据首先求出BQ的长,再利用y=S△BPQ+S△BEQ,得出答案即可;
③根据②中所求,结合一元二次方程的解法得出即可.
②根据首先求出BQ的长,再利用y=S△BPQ+S△BEQ,得出答案即可;
③根据②中所求,结合一元二次方程的解法得出即可.
解答:解:①∵在菱形ABCD中,AC=8cm,BD=6,
∴AO=CO=4cm,BO=DO=3cm,AC⊥BD,
∴AD=
=5(cm),
∵点P在线段AO上运动,点P从点A开始沿AC方向以每秒2cm的速度运动,
∴AP=2x,
∴OP=4-2x;
②∵四边形PBEQ的面积为y,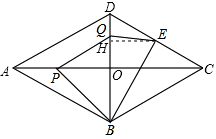
过点E作EH⊥BD,∵E为CD边中点,∴EH为△COD的中位线,
∴EH=
CO=2cm,
∵DQ=x,∴BQ=6-x,
∴y=S△BPQ+S△BEQ=
×(6-x)(4-2x)+
×(6-x)×2
=x2-9x+18;
③当四边形PBEQ的面积为13时,
则13=x2-9x+18,
整理得出:x2-9x+5=0,
解得:x1=
(此时P点在OC上,不合题意舍去),x2=
,
故x=
时,四边形PBEQ的面积为13.
∴AO=CO=4cm,BO=DO=3cm,AC⊥BD,
∴AD=
| 32+42 |
∵点P在线段AO上运动,点P从点A开始沿AC方向以每秒2cm的速度运动,
∴AP=2x,
∴OP=4-2x;
②∵四边形PBEQ的面积为y,

过点E作EH⊥BD,∵E为CD边中点,∴EH为△COD的中位线,
∴EH=
| 1 |
| 2 |
∵DQ=x,∴BQ=6-x,
∴y=S△BPQ+S△BEQ=
| 1 |
| 2 |
| 1 |
| 2 |
=x2-9x+18;
③当四边形PBEQ的面积为13时,
则13=x2-9x+18,
整理得出:x2-9x+5=0,
解得:x1=
9+
| ||
| 2 |
9-
| ||
| 2 |
故x=
9-
| ||
| 9 |
点评:此题主要考查了四边形的综合应用以及菱形的性质和一元二次方程的解法等知识,根据已知得出OP,BQ的长是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
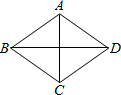 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
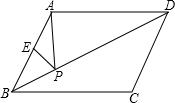
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.