题目内容
【题目】某校举办初中生数学素养大赛,比赛共设四个项目:七巧拼图、趣题巧解、数学应用和魔方复原,每个项目得分都按一定百分比折算后记入总分,并规定总分在85分以上(含85分)设为一等奖.下表为甲、乙、丙三位同学的得分情况(单位:分),其中甲的部分信息不小心被涂黑了.
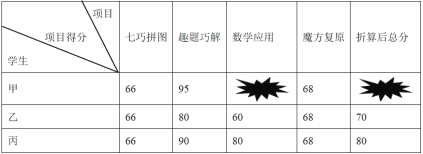
据悉,甲、乙、丙三位同学的七巧拼图和魔方复原两项得分折算后的分数之和均为20分.设趣题巧解和数学应用两个项目的折算百分比分别为x和y,请用含x和y的二元一次方程表示乙同学“趣题巧解和数学应用”两项得分折算后的分数之和为_________________;如果甲获得了大赛一等奖,那么甲的“数学应用”项目至少获得_________分.
【答案】![]() 或
或![]() 90
90
【解析】
(1)根据加权平均数的定义即可列出含x和y的二元一次方程;
(2)先根据乙和丙的折算分列方程组求出x和y的值,再根据“85分以上(含85分)设为一等奖”列不等式求解即可.
(1)由题意得
![]() 或
或![]() ;
;
(2)由题意得
![]() ,
,
解得
![]() .
.
设甲的数学应用得了m分,由题意得
95×0.4+0.3m≥85-20,
解得m≥90,
∴甲的“数学应用”项目至少获得90分.

练习册系列答案
相关题目